Предмет: Геометрия,
автор: stariklorenso
даю 50 баллов
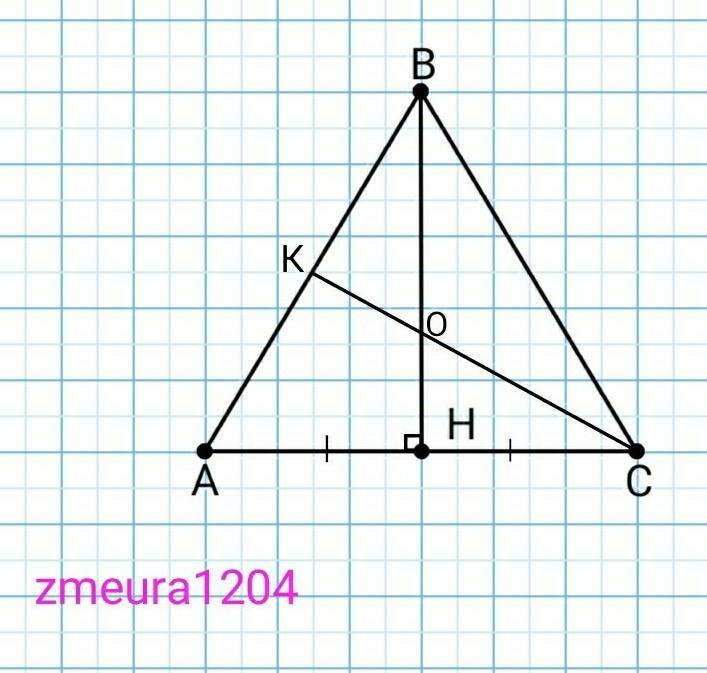
Задача. в равнобедренном треугольнике ABC AB = BC = 13 , AC = 10CM . Найти расстояние от точки пересечения медиан до каждой из вершин треугольника
Ответы
Автор ответа:
0
Ответ:
ВО=8см
СО=2√10,25 см
АО=СО=2√10,25 см
Объяснение:
BH- высота, медиана равнобедренного треугольника.
АН=НС; ВН- медиана.
АН=АС/2=10/2=5см
∆АВН- прямоугольный треугольник.
По теореме Пифагора:
ВН=√(АВ²-АН²)=√(13²-5²)=12см.
Медианы точкой пересечения делятся в отношении 2:1 начиная от вершины.
ВО:ОН=2:1
2+1=3 части
ВН:3=12:3=4см ОН
ВО=2*ОН=2*4=8см
cos∠A=AH/AB=5/13
AK=KB;
AK=AB/2=13/2=6,5 см.
Теорема косинусов:
КС=√(АК²+АС²-2*АК*АС*cos∠A)=
=√(6,5²+10²-2*6,5*10*5/13)=√(42,25+100-50)=
=√92,25 см
СО:ОК=2:1
СО=КС:3*2=2√92,25/3 см
Приложения:
zmeura1204:
Ещё и нарушение получили.
Похожие вопросы
Предмет: Химия,
автор: sadovskujvlad
Предмет: Алгебра,
автор: ievleva650
Предмет: Математика,
автор: alinamirzaeva735
Предмет: Математика,
автор: Аноним
Предмет: ОБЖ,
автор: rimmadancer