Question

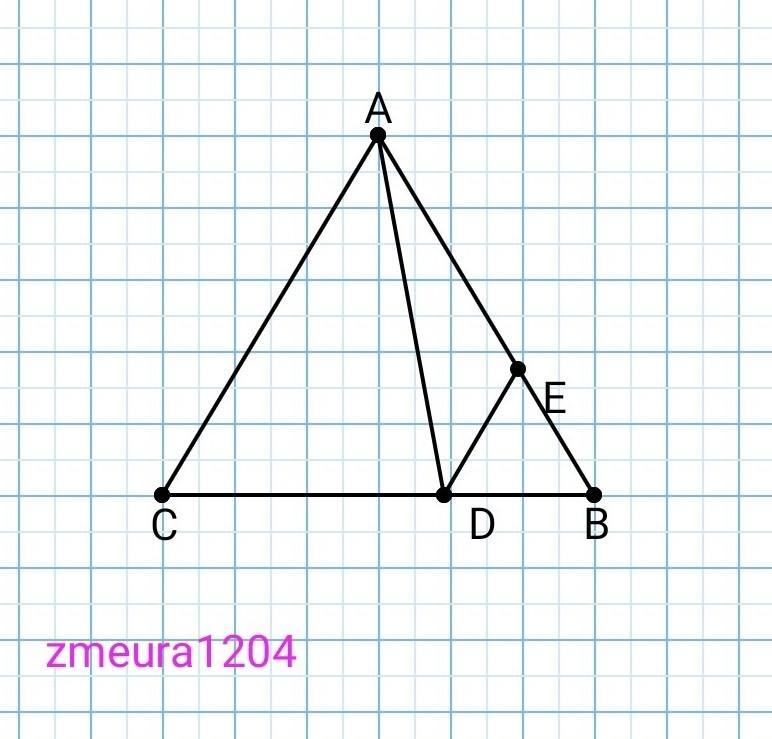
В правильном треугольнике АВС сторона равна 6 см. Точка D делит сторону ВС на отрезки BD=2 см и DC=4 см. Вычислите периметр треугольника ADE, если DЕ || AC, а точка Е принадлежит стороне АВ ​

Answer 1

Ответ:

Р(∆АDE)=6+2√7 см

Объяснение:

∆EBD~∆ABC, по углам.

ВD/BC=ED/AC

ED=BD*AC/BC=2*6/6=2 см.

ЕD=ВD=2см

∠В=60°;

В равнобедренном треугольнике углы при основании равны:

∠DEB=(180°-∠B)/2=(180°-60°)/2=60°

∆ЕВD- равносторонний треугольник, все углы по 60°

ЕВ=ED=BD=2см.

АЕ=AB-EB=6-2=4см.

∠АЕD=∠AEB-∠DEB=180°-60°=120°

По теореме косинусов:

AD=√(AE²+ED²-2*AE*ED*cos∠AED)=

=√(2²+4²-2*2*4*(-½))=√(4+16+8)=√28=2√7см

Р(∆ADE)=AD+DE+AE=2+4+2√7=6+2√7 см