Предмет: Математика,
автор: baloqlanovaayselcom
помогите Пж пж дам 15 баллов
а-b=7
ab= -5
----------
a^3+b^3=?
a^3-b^3=?
и другое пример:
(4c-1)^2-(2c+3)^2
Приложения:
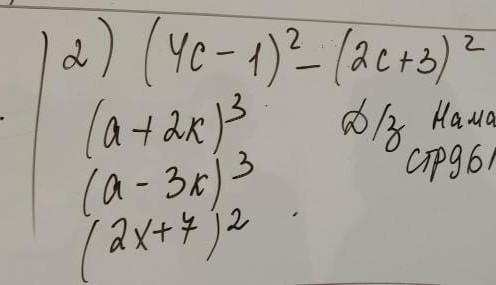
Ответы
Автор ответа:
0
Решение системы
Вычисления
Тут я воспользовался суммой и разностью кубов, второя скобка не имеет знания, так как первый множитель равен нулю
Похожие вопросы
Предмет: Алгебра,
автор: dda908298
Предмет: Литература,
автор: sofkaa12
Предмет: Геометрия,
автор: Аноним
Предмет: Алгебра,
автор: Kivor123
Предмет: Геометрия,
автор: qawaearra12341234