Question

Срочно нужна помощь
Даю 20 баллов

Answer 1

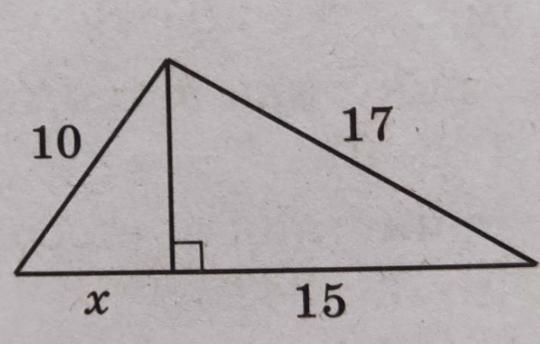
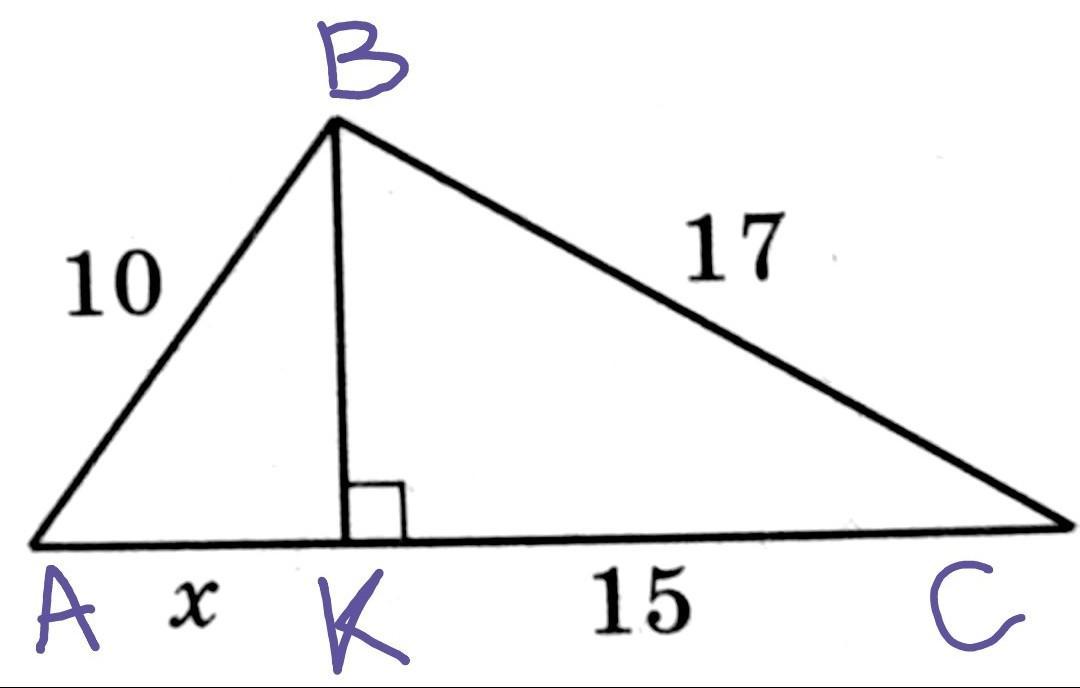
Для удобства обозначим буквами вершины треугольника.

Дано:

треугольник ABC,

BK перпендикулярно AC,

AB = 10, BC = 17, KC = 15

Найти: AK

Решение:

Перпендикуляр BK делит треугольник ABC на два прямоугольных треугольника — ABK и BCK.

Воспользуемся Теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (Гипотенуза — сторона прямоугольного треугольника, находящаяся напротив прямого угла).

Рассмотрим треугольник BCK.

По Теореме Пифагора:

BC${}^{2}$ = BK${}^{2}$ + KC${}^{2}$

BK${}^{2}$ = BC${}^{2}$ – KC${}^{2}$ = 17${}^{2}$ – 15${}^{2}$ =

= (17 – 15)(17 + 15) = 2 × 32 = 64 = 8${}^{2}$

BK = 8

Теперь рассмотрим треугольник ABK.

По той же Теореме Пифагора:

AB${}^{2}$ = AK${}^{2}$ + BK${}^{2}$

AK${}^{2}$ = AB${}^{2}$ – BK${}^{2}$ = 10${}^{2}$ – 8${}^{2}$ =

= (10 – 8)(10 + 8) = 2 × 18 = 36 = 6${}^{2}$

AK = 6

Ответ: 6