Question

У рівнобедреному трикутнику радіус вписаного кола дорівнює 4 см а кут при основі - 36° виразіть основу

Answer 1

Ответ:

$\displaystyle AC=\frac{8}{tg\;18^0}$

АС = 25 см

Объяснение:

В равнобедренном треугольнике радиус вписанной окружности равен 4 см, а угол при основании 36°. Выразите основание.

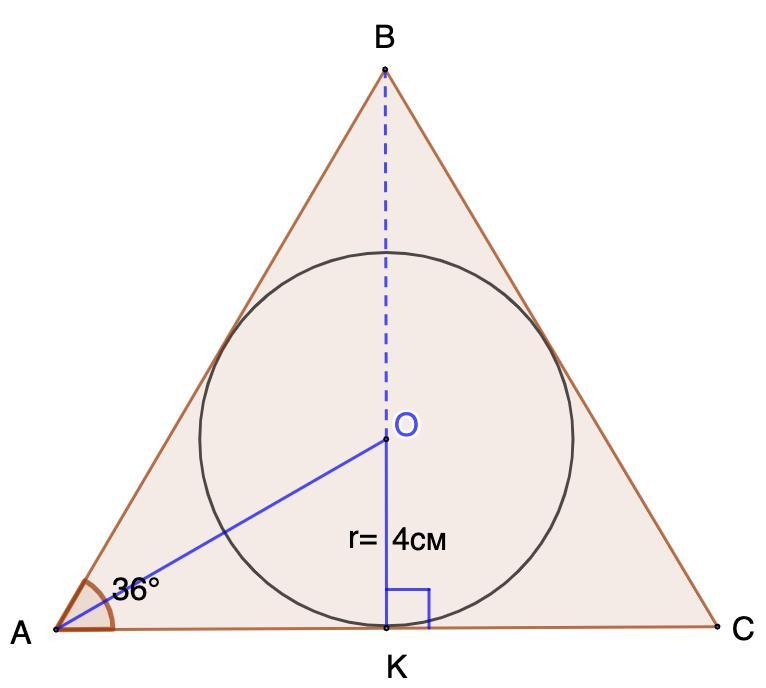
Дано: ΔАВС - равнобедренный;

∠А = 36°;

Окр.(О, r) - вписанная;

r = 4 см.

Выразить основание.

Решение:

• Радиус вписанной окружности лежит на биссектрисе угла.

⇒ ∠ВАО = ∠ОАК = 36° : 2 = 18°

Рассмотрим ΔАОК.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОК ⊥ АС  ⇒  ΔАОК - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg\angle OAK = \frac{OK}{AK} \\\\AK = \frac{OK}{tg\angle OAK} =\frac{4}{tg\;18^0}$

Рассмотрим ΔАВС - равнобедренный.

ВК - высота.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ АК = КС.

$\displaystyle AC=2\cdot \frac{4}{tg\;18^0} =\frac{8}{tg\;18^0}$

tg 18° ≈ 0,32

⇒ AC ≈ 25 см.

#SPJ1