Question

докажите, что медиана ае треугольника авс меньше полусуммы двух соседних его сторон​

Answer 1

Ответ:

Доказано требуемое.  

Объяснение:

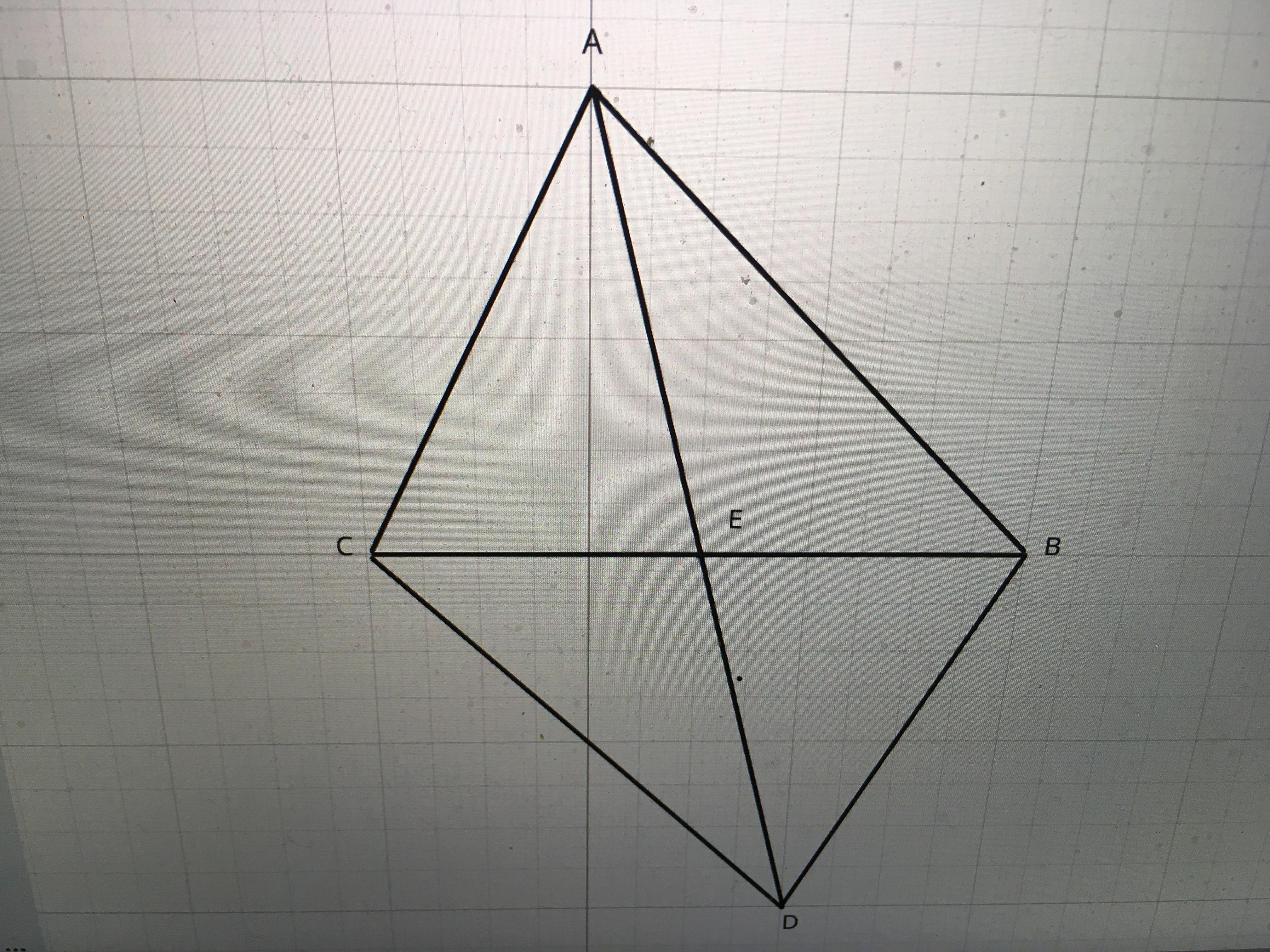
Продолжим медиану AE за точку E до точки D так, чтобы AE=ED. Соединим точки B и D, С и D; получаем четырехугольник ABDC. Поскольку по построению его диагонали в точке пересечения делятся пополам, это параллелограмм, поэтому BD=AC. Как известно, в треугольнике сумма двух сторон всегда больше третьей (это так называемое неравенство треугольника), поэтому

                                   AB+BD>AD⇒AB+AC>2AE,

что и требовалось доказать.

Answer 2

Ответ:

Достаточно достроить это все до параллелограмма (АБСД), где по свойству диагонали делятся точкой пересечения пополам, а также БД = АС, ДС = АБ по построению (параллелограмм)

Потому АЕ будет равно половине диагонали АД.

Далее рассматриваем треугольник АБД.

Как известно любые 2 стороны треугольника больше третьей (ломаная всегда больше чем отрезок с теми же концами). Поэтому АБ + БС > АД

АД = 2АЕ

Откуда, (АБ + БС)/2 > АЕ