Question

Геометрия
очень срочно с объяснением

Answer 1

Ответ: 47°; 38°.

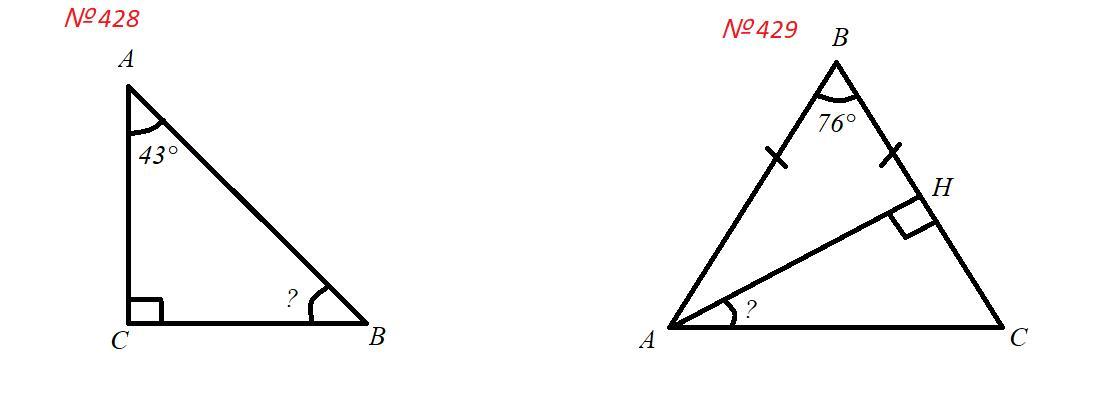
Задача 428.

Один из острых углов прямоугольного прямоугольника равен 43°. Найдите другой острый угол.

Дано: ΔСАВ - прямоугольный, ∠С = 90°, ∠А = 43°

Найти: ∠В

Решение:

Сумма острых углов в прямоугольном треугольнике = 90° ⇒

⇒ ∠В = ∠С - ∠А = 90° - 43° = 47°

проверим: 43° + 47° = 90° Верно.

Ответ: ∠В = 47°.

Задача 429.

В равнобедренном треугольнике ABC (AB = BC) проведена высота AH. Найдите угол CAN, если угол B =76°

Дано: ΔАВС, АВ = ВС, АН - высота, ∠В = 76°.

Найти: ∠САН.

Решение:

1) ΔАВС - равнобедренный треугольник, поскольку АВ=ВС, значит углы при основании этого треугольника равны, т.е ∠А=∠С;

2) Т.к сумма углов треугольника = 180°, то ∠А=∠С= (180° - 76°)/2 =

= 104°/2 = 52°;

3) Р/м ΔАНС - прямоугольный, т.к. АН - высота ⇒ АН ⊥ ВС, значит

∠Н = 90°;

4) Сумма острых углов = 90°, тогда ∠САН = ∠АНС - ∠НСА = 90° - 52° =

= 38°.

Ответ: ∠САН = 38°.