Question

Довжини основ рівнобічної трапеції – 25 см і 55 см. Довжина висоти, опущеної з вершини тупого кутана більшу основу, дорівнює 36см. Знайдіть довжину бічної сторони трапеції.
Допомжіть даю 30 балів!!!!!!!!!!!!!!!!!

Answer 1

Ответ:

Бічна сторона трапеції дорівнює 39 см

Объяснение:

Довжини основ рівнобічної трапеції – 25 см і 55 см. Довжина висоти, опущеної з вершини тупого кутана більшу основу, дорівнює 36см. Знайдіть довжину бічної сторони трапеції.

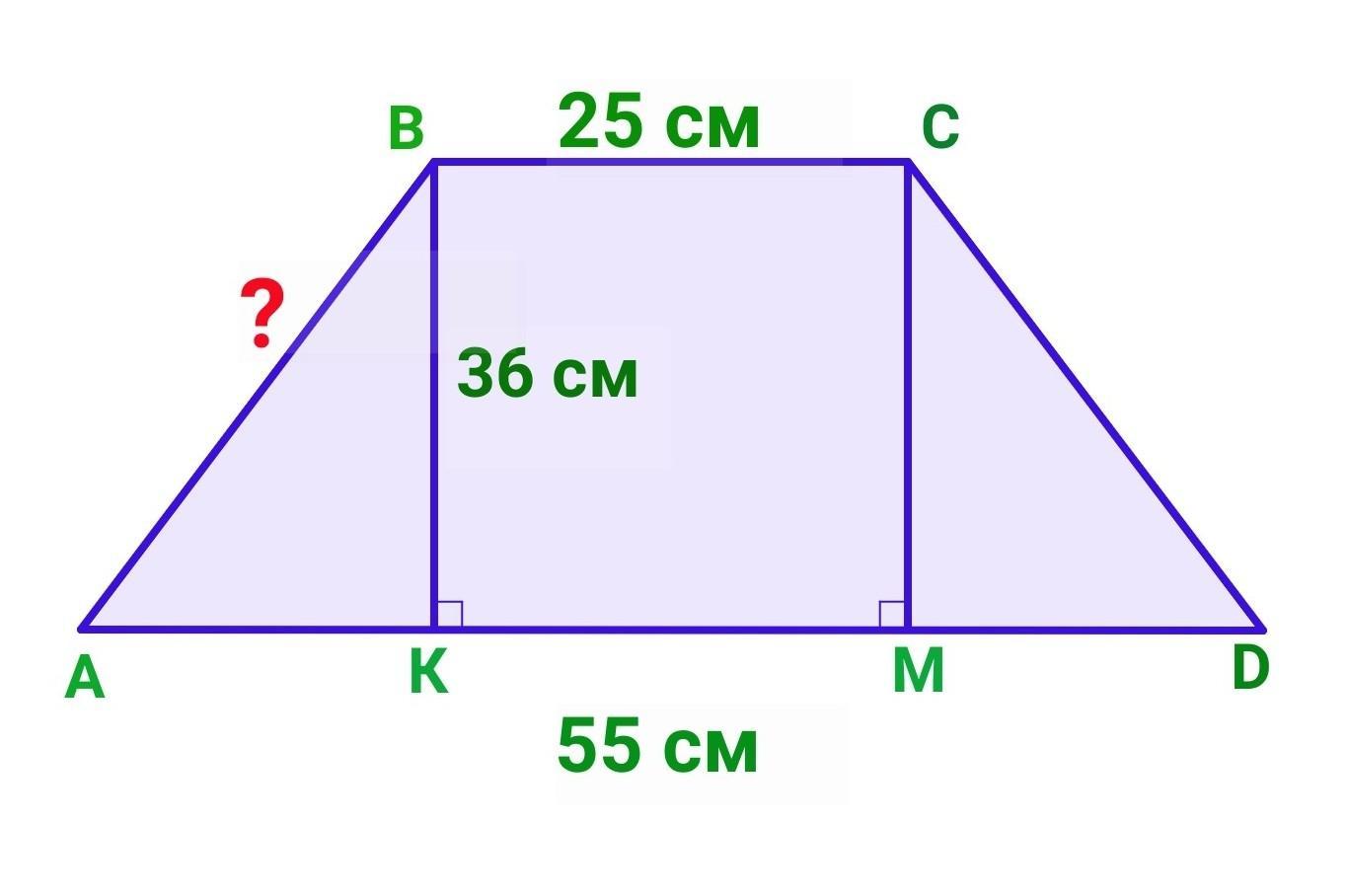
Нехай ABCD - дана трапеція (BC || AD), у якої основи BC=25 см, AD=55 см; бічні сторони AB=CD.

1.

Проведемо дві висоти ВК і СМ.

△ABK=△DCM (за катетом і гострим кутом):

• BK=CM - як висоти трапеції
• ∠A=∠D - як кути при основі рівнобічної трапеції

Отже AK=DM - як відповідні сторони рівних трикутників.

2.

Оскільки BCMK - прямокутник, то KM=BC=25 (см)

Маємо:

$\sf AK=DM = \dfrac{AD - KM}{2} = \dfrac{AD - BC}{2} = \dfrac{55 - 25}{2} = \bf 15$ (см)

3.

Розглянемо прямокутний трикутник АВК (∠АКВ=90°)

За теоремою Піфагора знайдемо гіпотенузу АВ:

$\sf AB = \sqrt{ {AK}^{2} + {BK}^{2} } = \sqrt{ {15}^{2} + {36}^{2} } = \sqrt{1296 + 225} = \sqrt{1521} = \bf39$ (см)

Відповідь: 39 см

#SPJ1