Предмет: Алгебра,
автор: orosyarik
Приложения:

Ответы
Автор ответа:
1
Ответ:
надеюсь почерк разберёшь
Приложения:
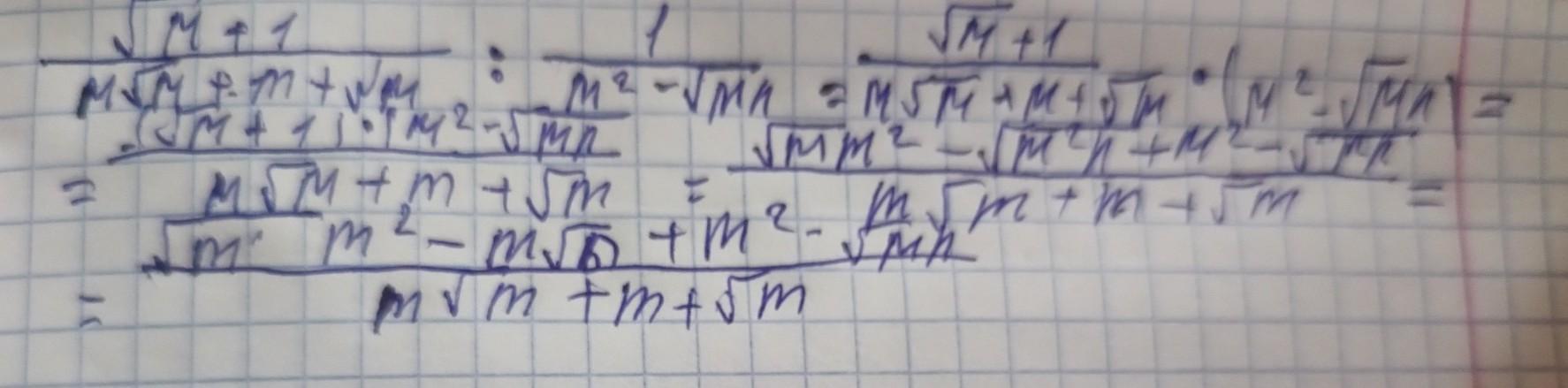
orosyarik:
так дякую
Автор ответа:
1
Объяснение:
Пусть √m=t ⇒
m=t² m²=(t²)²=t⁴.
помогите пожалуйста с алгеброй в моём профиле, буду очень благодарен
Похожие вопросы
Предмет: Математика,
автор: bidashaleksandra
Предмет: Математика,
автор: mirtoirovaholida
Предмет: Английский язык,
автор: orazgulgauhar08
Предмет: История,
автор: ctrlshiftt
Предмет: Математика,
автор: dashadidenko32