Предмет: Алгебра,
автор: samsunglilya1985
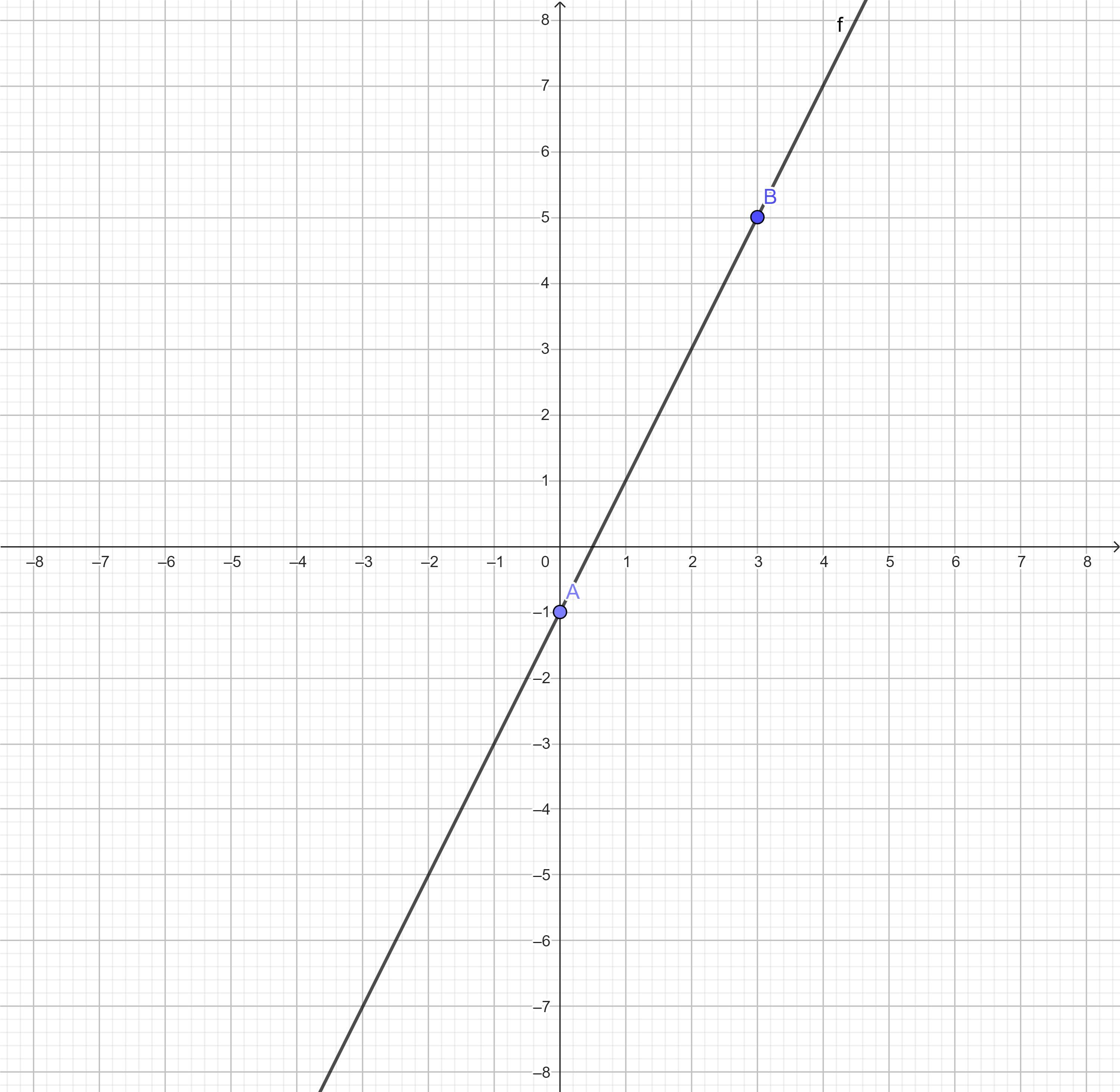
графік функції пряма, що проходить через точку А(0;-1) і В(3;5). задати за допомогою формули цю функцію. Потрібна повна відповідь
Ответы
Автор ответа:
52
График функции прямая, проходящая через точку А(0;-1) и В(3;5). Задать эту функцию с помощью формулы.
Ответ:
y = 2x - 1
Объяснение:
Уравнение прямой можно записать в виде y = kx + b.
Для того чтобы найти эти коэффициенты, необходимо использовать координаты точек A и B.
Коэффициент наклона k равен разности y-координат двух точек, разделенной на разность x-координат этих точек:
Коэффициент смещения b можно найти, подставив значения координат одной из точек и найденное значение k:
y = kx + b
-1 = 2 * 0 + b
b = -1
Таким образом, уравнение прямой, проходящей через точки A(0;-1) и B(3;5), будет выглядеть следующим образом:
y = 2x - 1.
Приложения:
cnezaart128:
спасибо большое точнее огромное!
откуда появилось (-1)
Похожие вопросы
Предмет: Информатика,
автор: vitaliiandryuk1
Предмет: Математика,
автор: sutkafilip
Предмет: Геометрия,
автор: wixmind
Предмет: Математика,
автор: agafonoff82
Предмет: Математика,
автор: artemch100