Предмет: Математика,
автор: aleksejsavickij699
Составить уравнение касательной к графику функции в заданной точке.
Приложения:
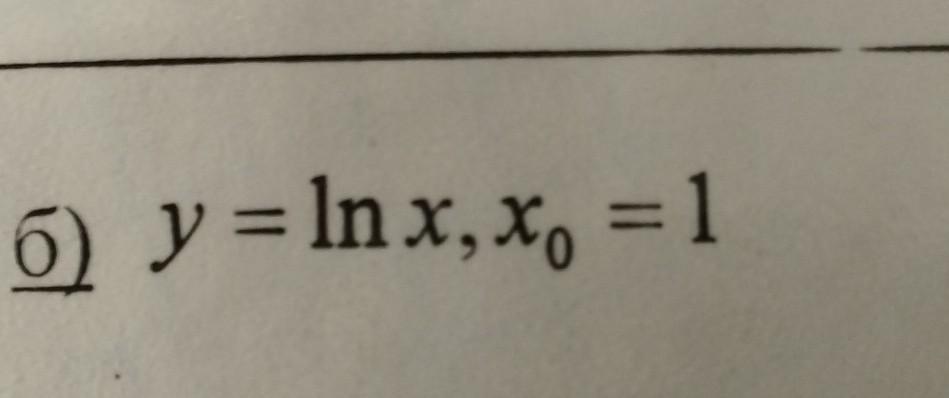
Ответы
Автор ответа:
0
Чтобы найти уравнение касательной к графику функции в заданной точке, нам нужно найти производную функции в этой точке, а затем использовать ее для нахождения уравнения касательной.
Первоначально найдем производную функции:
y = In x
y' = 1/x
Затем найдем значение производной в заданной точке x0 = 1:
y'(1) = 1/1 = 1
Таким образом, наклон касательной к графику функции в точке x0 = 1 равен 1.
Теперь нам нужно найти уравнение касательной, используя найденный наклон и координаты заданной точки (1, In 1):
y - In 1 = 1(x - 1)
y - In 1 = x - 1
y = x + In 1 - 1
y = x - 1
Таким образом, уравнение касательной к графику функции y = In x в точке x0 = 1 равно y = x - 1.
Первоначально найдем производную функции:
y = In x
y' = 1/x
Затем найдем значение производной в заданной точке x0 = 1:
y'(1) = 1/1 = 1
Таким образом, наклон касательной к графику функции в точке x0 = 1 равен 1.
Теперь нам нужно найти уравнение касательной, используя найденный наклон и координаты заданной точки (1, In 1):
y - In 1 = 1(x - 1)
y - In 1 = x - 1
y = x + In 1 - 1
y = x - 1
Таким образом, уравнение касательной к графику функции y = In x в точке x0 = 1 равно y = x - 1.
Похожие вопросы
Предмет: Математика,
автор: Sigma60fps
Предмет: Информатика,
автор: Аноним
Предмет: Физика,
автор: charlwxn
Предмет: История,
автор: lfmfijindjdsi