Предмет: Геометрия,
автор: alesamamontova643
2. 3 точки до площини проведено похилу завдовжки 6 см. Знайдіть кут, який утворює похила з площиною, якщо проєкцiя похилоï до- рiвнює 3/3 см.
Ответы
Автор ответа:
4
Ответ:
∠(АВ;α) = 30°
Объяснение:
С точки к плоскости проведена наклонная, длиной 6 см. Найдите угол, который образует наклонная с плоскостью, если проекция наклонной равна 3√3 см.
------------------------------------------------------
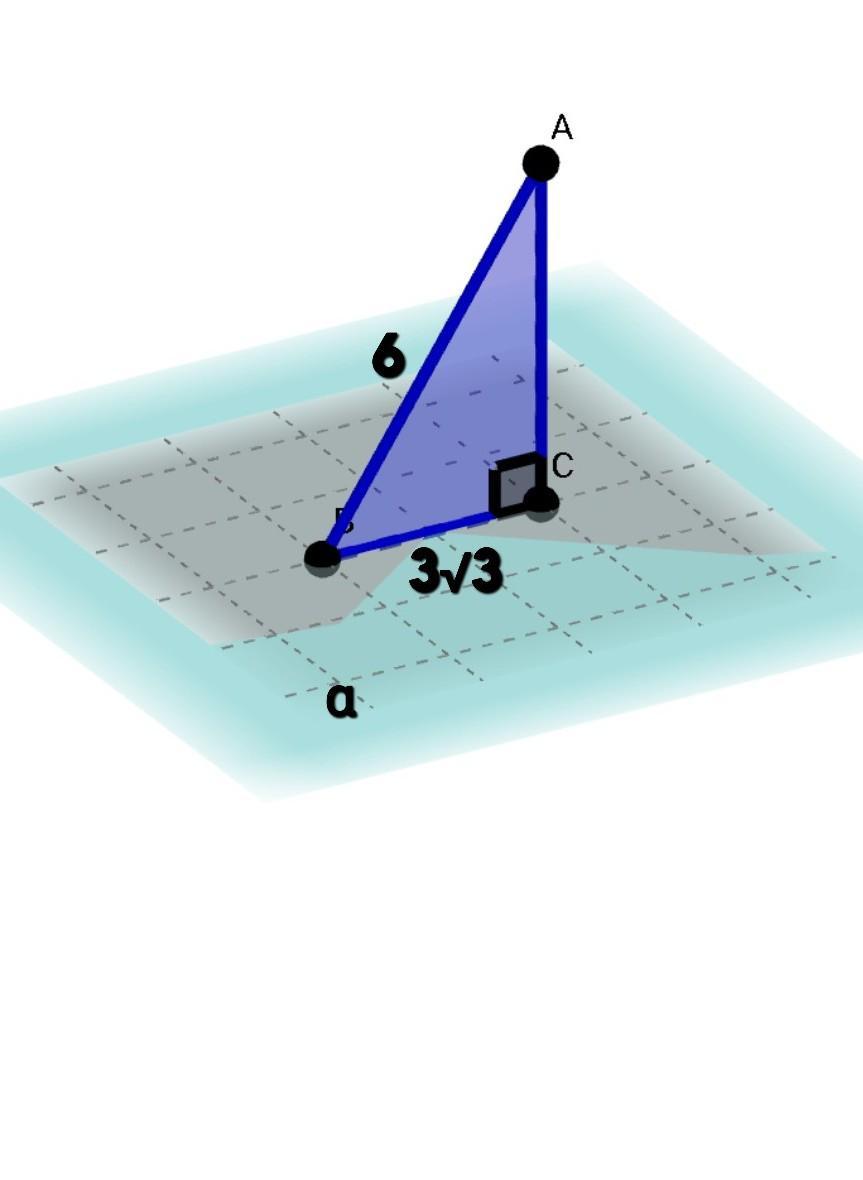
Дано: Пусть α - плоскость, АВ - наклонная, АС - перпендикуляр, ВС - проекция наклонной, ∠С = 90°, АВ = 6см, ВС = 3√3см
Найти: ∠(АВ;α)
⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией. ∠(АВ;α) =∠АВС
- Косинус ∠АВС равен отношению прилежащего катета(ВС) к гипотенузе(АВ).
∠АВС = 30°
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mariatoo625
Предмет: Математика,
автор: sevcenkoveronika792
Предмет: Другие предметы,
автор: kiradzipetryk
Предмет: История,
автор: khomyakovd123
Предмет: Русский язык,
автор: nargizabafaeva542