Предмет: Алгебра,
автор: annafilinuk0
хто може вирішити їх даю 100 балів
Приложения:
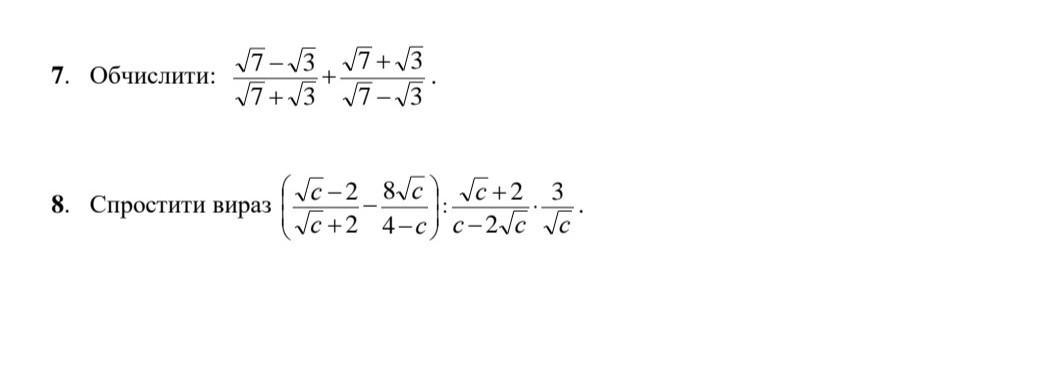
Ответы
Автор ответа:
1
Ответ:
Применяем формулы разности квадратов , а также квадрата суммы и квадрата разности .
Похожие вопросы
Предмет: Математика,
автор: darinadrobisheva2010
Предмет: Другие предметы,
автор: 05anikinavalentina07
Предмет: Английский язык,
автор: komola08
Предмет: Математика,
автор: fatiyeva084
Предмет: Литература,
автор: egormaksim10