Предмет: Алгебра,
автор: PRZEPRASZAM
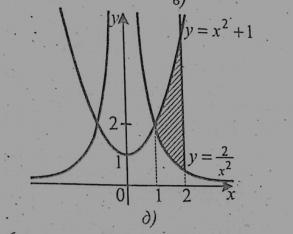
Обчисліть площу заштрихованої фігури зображеної на рисунку:
Приложения:
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
Для знаходження площі заштрихованої фігури потрібно від площі однієї фігури(та що вище) відняти площу іншої(та що нижче) з вказаними межами:
Похожие вопросы
Предмет: Литература,
автор: 1nsultzxc666
Предмет: Английский язык,
автор: mmeerim793
Предмет: Английский язык,
автор: BMZH1B
Предмет: Физкультура и спорт,
автор: wordyou
Предмет: Литература,
автор: protuberanec2018