буду благодарна всей душой!!! параллелограммы меня уже убивают
дано :
угол А = 90°
ВА=АС
ADEF - прямоугольник
S(BDE) = a
S(EFC) =b
доказть : S(ADEF)=

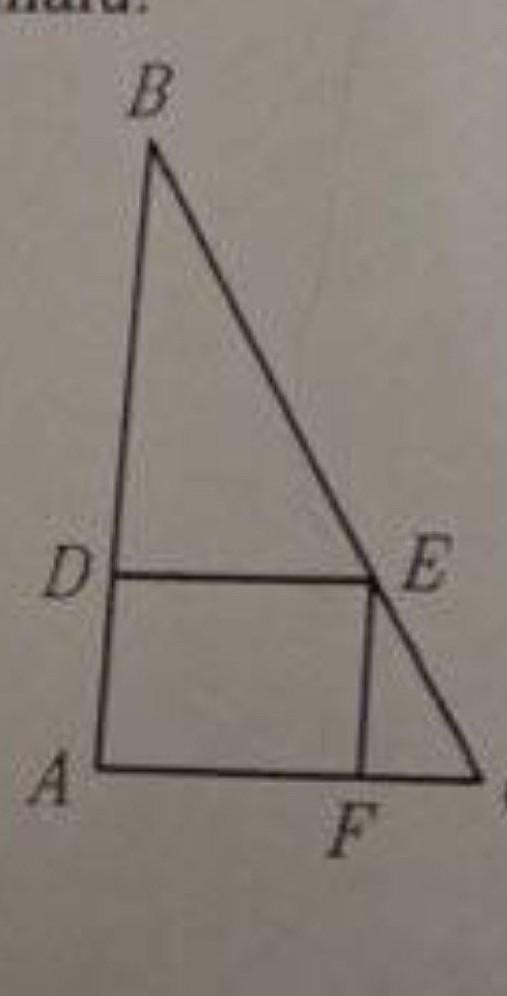
Ответы
Ответ:
Чтобы доказать, что S(ADEF) = 2√ab, мы можем использовать теорему Пифагора и свойства прямоугольника.
Во-первых, поскольку угол А = 90°, то треугольник ABC прямоугольный. Из этого следует, что AB² + BC² = AC² (теорема Пифагора).
Заметим, что AB = AC/2, так как ВА=АС. Поэтому можно переписать уравнение выше в виде AB² + (2AB)² = AC².
Раскрывая скобки, получаем 5AB² = AC². Теперь заметим, что прямоугольник ADEF можно разбить на два прямоугольных треугольника: ADE и AEF. Оба эти треугольника имеют гипотенузу AC, а катеты AD и DE равны BC, а катеты AF и EF равны AB.
Теперь мы можем выразить S(ADE) и S(AEF) через AB и BC, используя формулу для площади прямоугольного треугольника: S = (1/2) * катет1 * катет2.
S(ADE) = (1/2) * BC * AB = (1/2) * AC * AB/2 = (1/4) * AC * AB.
S(AEF) = (1/2) * AB * AC/2 = (1/4) * AC * AB.
Теперь мы можем выразить S(ADEF) через S(ADE) и S(AEF):
S(ADEF) = S(ADE) + S(AEF) = (1/4) * AC * AB + (1/4) * AC * AB = (1/2) * AC * AB.
Но мы знаем, что 5AB² = AC², поэтому можно переписать S(ADEF) в виде:
S(ADEF) = (1/2) * AC * AB = (1/2) * AB * √(5AB²) = √(5/4) * AB².
Из этого следует, что S(ADEF) = 2√(AB² * 5/4) = 2√(AB² * (BC * AF)) = 2√ab.
Таким образом, мы доказали, что S(ADEF) = 2√ab