Question

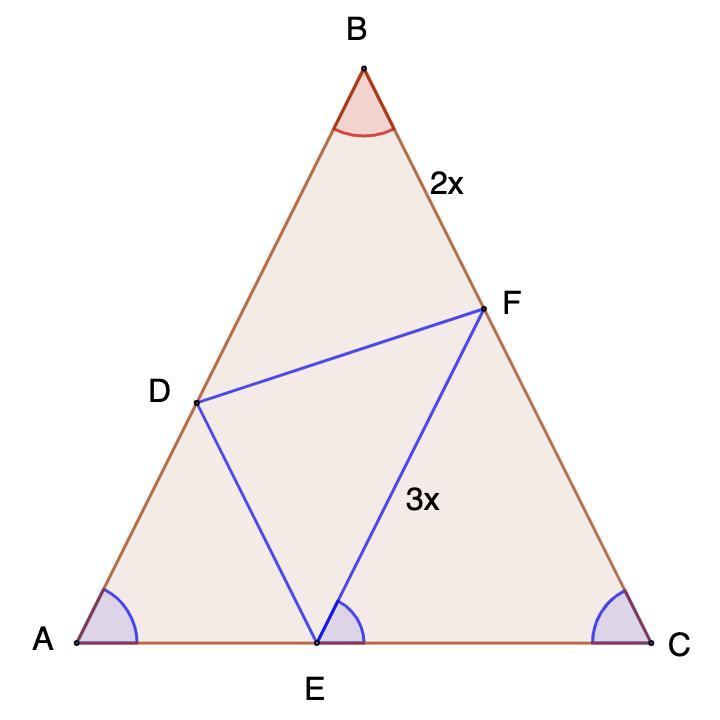
математика 11 клас //////На основании АС равнобедренного треугольника АВС взята точка Е, а на боковых сторонах АВ и ВС точки D и F так, что DE ‖ BC и EF ‖ AB. Какую часть площади треугольника АВС занимает площадь треугольника DEF, если BF:EF=2:3?

Answer 1

Ответ:

$\displaystyle \bf \frac{S(DFE)}{S(ABC)}=\frac{6}{25}$

Пошаговое объяснение:

На основании АС равнобедренного треугольника АВС взята точка Е, а на боковых сторонах АВ и ВС точки D и F так, что DE ‖ BC и EF ‖ AB. Какую часть площади треугольника АВС занимает площадь треугольника DEF, если BF:EF=2:3?

Дано: ΔАВС - равнобедренный;

D ∈ AB; F ∈ BC;

DE ‖ BC;  EF ‖ AB;

BF : EF = 2 : 3.

Найти: S(DEF) : S(ABC)

Решение:

BF : EF = 2 : 3

Пусть BF = 2х; тогда EF = 3х.

Рассмотрим ΔЕFC.

∠А = ∠С (при основании равнобедренного треугольника)

∠А = ∠FEC (соответственные при DE ‖ BC и секущей АС)

⇒ ∠С = ∠FEC

• Если два угла в треугольнике равны, то этот треугольник - равнобедренный.

⇒ EF = FC = 3x.

Рассмотрим ΔАВС - равнобедренный.

АВ = ВС = 2х + 3х = 5х

Площадь ΔАВС найдем по формуле:

                $\displaystyle \bf S=\frac{1}{2}ab\;sin\;\alpha$ ,

гда a и b - стороны треугольника; α - угол между ними.

$\displaystyle \bf S(ABC)=\frac{1}{2} AB\cdot BC\cdot sinB=\frac{1}{2}\cdot5x \cdot 5x \cdot sinB =\frac{25x^2sinB}{2}$

Рассмотрим DBFE.

DE ‖ BC;  EF ‖ AB

⇒ DBFE - параллелограмм (по определению)

• Противоположные стороны параллелограмма равны.

⇒ FE = DB = 3x.

• Площадь DBFE найдем по формуле:

                            $\displaystyle \bf S=ab\;sin\;\alpha$ ,

гда a и b - стороны параллелограмма; α - угол между ними.

$\displaystyle \bf S(DBFE)=DB\cdot BF\cdot sinB=3x \cdot 2x\cdot sinB=6x^2sinB$

• Диагональ делит параллелограмм на два равновеликих треугольника.

⇒ $\displaystyle \bf S (DFE)=S(DBFE) : 2 = 6x^2sinB : 2 = 3x^2sinB$

Найдем, какую часть площади треугольника АВС занимает площадь треугольника DEF:

$\displaystyle \bf \frac{S(DFE)}{S(ABC)}=\frac{3x^2sinB\cdot2}{25x^2sinB}=\frac{6}{25}$