Предмет: Геометрия,
автор: valerialera455
помогите, очень срочно нужно!!
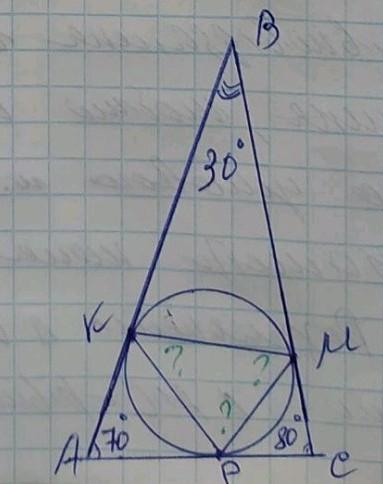
У трикутник з кутами 30°, 70° і 80° вписано коло.
Знайдіть кути трикутника, вершини якого є точками
дотику вписаного кола до сторін даного трикутника.
Приложения:
Ответы
Автор ответа:
3
Ответ: 50°; 55°; 75°
Объяснение:
Дано:
∆ABC, < (кут) BAC = 70°, < ABC = 30°, < BCA= 80°,
точки торкання кола і сторін ∆ KMP;
Знайти:
<KPM y ∆KPM
Розв'язання
За якістю відрізків дотичних,проведених з однієї точки до кола. ∆ KBM, MCP та AKP - рівнобедрені. Сума кутів трикутника 180°. У ∆KBM кути при КМ рівні <KBM = <BMI = (180° - 30°) : 2 = 75°.
У ∆PMC кути при MP рівні
<MPC= <PMC = (180° - 80°) : 2 = 50°
У ∆ PAK кути при PK рівні <AKP=<KPA = (180°-70°):2 = 55°. <BMC розгорнутий.
<KPM = 180° - < MPC - < KPA = 180° - 50° - 55° = 75°
<MKP= 180° - <BKM - <AKP = 180° - 75° - 55° = 50°
Відповідь: < MKP = 50°; <KMP = 55° ;
< KPM = 75°
valerialera455:
спасибо
Похожие вопросы
Предмет: Математика,
автор: aubakirovruslan53
Предмет: Английский язык,
автор: Аноним
Предмет: История,
автор: jxisjrbxks
Предмет: Литература,
автор: krista200659
Предмет: Окружающий мир,
автор: urijsapozenko33109