Предмет: Алгебра,
автор: bondarcukivan58
Знайдіть площу фігури, обмеженої параболою y= 2+x-x2 і прямою y=2-x.
Строчно
Ответы
Автор ответа:
1
Ответ:
Площадь фигуры, ограниченной параболой y = 2 + x - x² и прямой y = 2 - x равна кв. ед.
Объяснение:
Найдите площадь фигуры, ограниченной параболой y = 2 + x - x² и прямой y = 2 - x.
- Формула площади, ограниченной линиями:
Для начала найдем абсциссы точек пересечения графиков:
- Еще понадобится формула Ньютона - Лейбница:
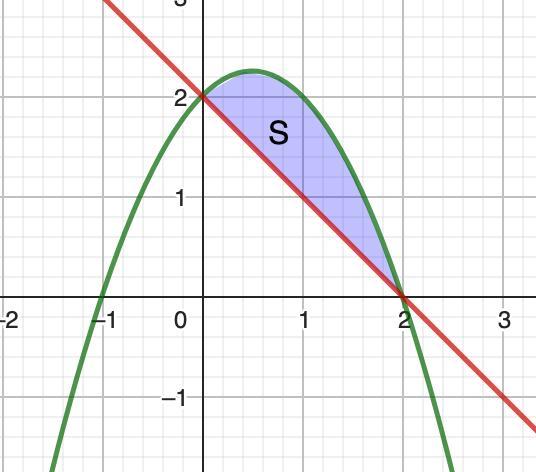
Построим схематично графики.
Имеем b = 2 (справа); a = 0 (слева); f₂(x) = 2 + x - x₂ (сверху); f₁(x) = 2 - x (снизу).
Подставим эти данные в функцию:
Площадь фигуры, ограниченной параболой y = 2 + x - x² и прямой y = 2 - x равна кв. ед.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Izazakhan
Предмет: Химия,
автор: areter222
Предмет: Химия,
автор: areter222
Предмет: Русский язык,
автор: zisabaev697
Предмет: История,
автор: Werlode