Предмет: Алгебра,
автор: 0954334453z
Даю 100 Балов Поиогите
Приложения:
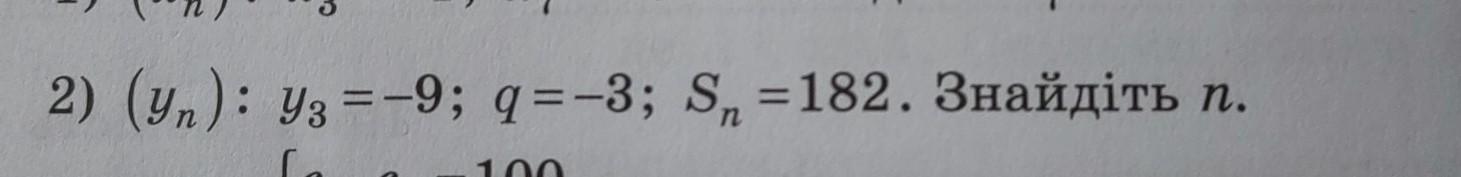
Ответы
Автор ответа:
0
Ответ: n=6 .
Геометрическая прогрессия :
Найдём первый член геометрической прогрессии .
Запишем сумму первых n-членов геом. прогрессии .
Похожие вопросы
Предмет: Биология,
автор: madinnka24
Предмет: Математика,
автор: ailin3279
Предмет: Математика,
автор: tamilasosidka11
Предмет: Английский язык,
автор: valerijtroshkin06
Предмет: Литература,
автор: tori5252