Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста с решением Найдите экстремум
Приложения:
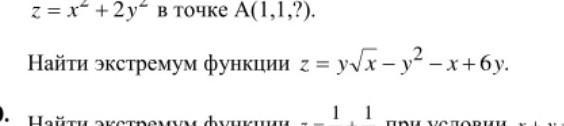
Ответы
Автор ответа:
1
Ответ: в точке К₁(4;4) имеется максимум z(4;4) =12.
Объяснение:
1. Найдём частные производные:
2. Решаем систему уравнений:
3. Найдём частные производные второго порядка:
4. Вычислим значение этих частных производных второго порядка в критической точке К₁(4;4):
В точке К₁(4;4) имеется максимум
z(4;4) =4*√4-4²-4+6*4=8-16-4+24=12.
Автор ответа:
1
Ответ:
Найдём стационарные точки . Для этого найдём частные
Стационарная точка .
Проверим достаточное условие экстремума функции двух переменных, для применения которого нужно вычислить частные производные 2-го порядка в точке М₀ .
Обозначения:
Вычислим значение выражения
Так как Δ>0 , то имеем экстремум в точке М₀(4;4) .
Это будет максимум, так как А<0 .
Максимум функции равен .
Похожие вопросы
Предмет: Экономика,
автор: nikitaderebo
Предмет: Алгебра,
автор: ogfyyuuu
Предмет: История,
автор: tujmebekerdaulet
Предмет: Қазақ тiлi,
автор: nastenka0895
Предмет: Математика,
автор: SadovNIKKK