ДУЖЕ ПОТРІБНО
cos^2x + tg^2x =1
Ответы
Ответ:
Розглянемо тотожність cos^2x + tg^2x = 1:
Для початку перетворимо тангенс до синуса та косинуса за допомогою тотожності tgx = sinx/cosx:
cos^2x + (sinx/cosx)^2 = 1
Помножимо обидві частини рівняння на cos^2x, щоб позбутися від знаменника:
cos^2x * cos^2x + sin^2x = cos^2x
Додамо sin^2x до обох боків рівняння:
cos^2x * cos^2x + sin^2x + sin^2x = cos^2x + sin^2x
Згрупуємо синуси разом та скористаємося тотожністю cos^2x + sin^2x = 1:
cos^2x * cos^2x + 2sin^2x = 1
Перенесемо cos^2x на один бік, а решту термінів на інший:
2sin^2x = 1 - cos^2x * cos^2x
Поділимо обидві частини рівняння на 2:
sin^2x = (1 - cos^2x * cos^2x) / 2
Отже, ми довели тотожність cos^2x + tg^2x = 1 і отримали альтернативний вираз для sin^2x, який можна використовувати, якщо потрібно позбутися від тангенса.
Объяснение:
cos^2x + tg^2x =1



(1-tg²x)/(1+tg²x)-2tgx/(1-tg²x)=1
(1-tg²x)²-2tgx(1+tg²x)=(1+tg²x)(1-tg²x)
1-2tg²x+tg⁴x-2tgx-2tg³x=1-tg⁴x
2tg⁴x-2tg³x-2tg²x-2tgx=0
2tgx(tg³x-tg²x-tgx-1)=0
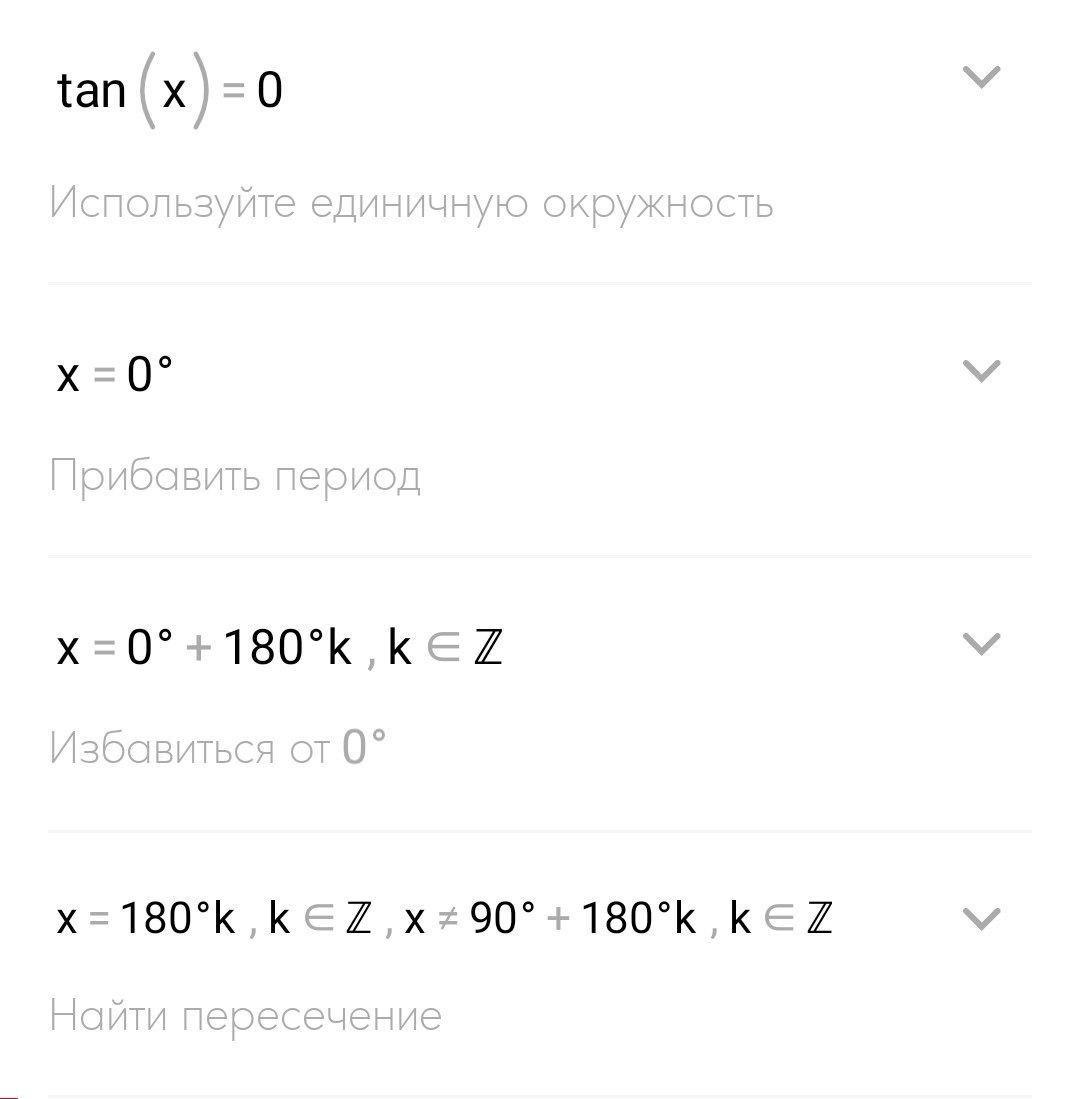
1)tgx=0
x=πk;k€Z
2)tg³x-tg²x-tgx-1=0
tgx(tg²x-1)-(tg²x+1)=0
1+tg²x#0;1-tg²x#0
-tgx(1-tg²x)-(1+tg²x)=0