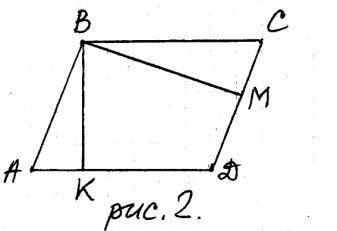
У паралелограмі (рис. 2) проведено висоти ВК і ВМ. Сторони паралелограма відносяться як 2:3. Знайти вк, якщо ВМ х 4 см.
Ответы
Ответ: За теоремою про висоту в паралелограмі, висота розділяє паралелограм на два півпаралелограма, площі яких дорівнюють половині площі всього паралелограма. Тому можемо записати:
Площа паралелограма = 2 * Площа півпаралелограма = 2 * Площа трикутника ВМК
Для знаходження площі трикутника ВМК нам потрібно знайти довжину його основи ВК. За умовою відомо, що сторони паралелограма відносяться як 2:3, тому можемо записати:
ВК : ВМ = 2 : 3
ВК = (2/3) * ВМ = (2/3) * 4 см = 8/3 см
Тепер ми знаємо довжини основи ВК і висоти ВМ, тому можемо обчислити площу трикутника ВМК:
Площа трикутника ВМК = (1/2) * ВК * ВМ = (1/2) * (8/3) см * 4 см = 32/3 см²
Таким чином, площа паралелограма дорівнює:
Площа паралелограма = 2 * Площа трикутника ВМК = 2 * (32/3) см² = 64/3 см²
А оскільки площа паралелограма відома, можемо знайти його другу основу ВК:
Площа паралелограма = ВК * ВМ
64/3 см² = (8/3) см * ВК
ВК = (64/3) см² / (8/3) см = 8 см
Отже, ВК дорівнює 8 см.
Пошаговое объяснение: