Предмет: Алгебра,
автор: babovbez
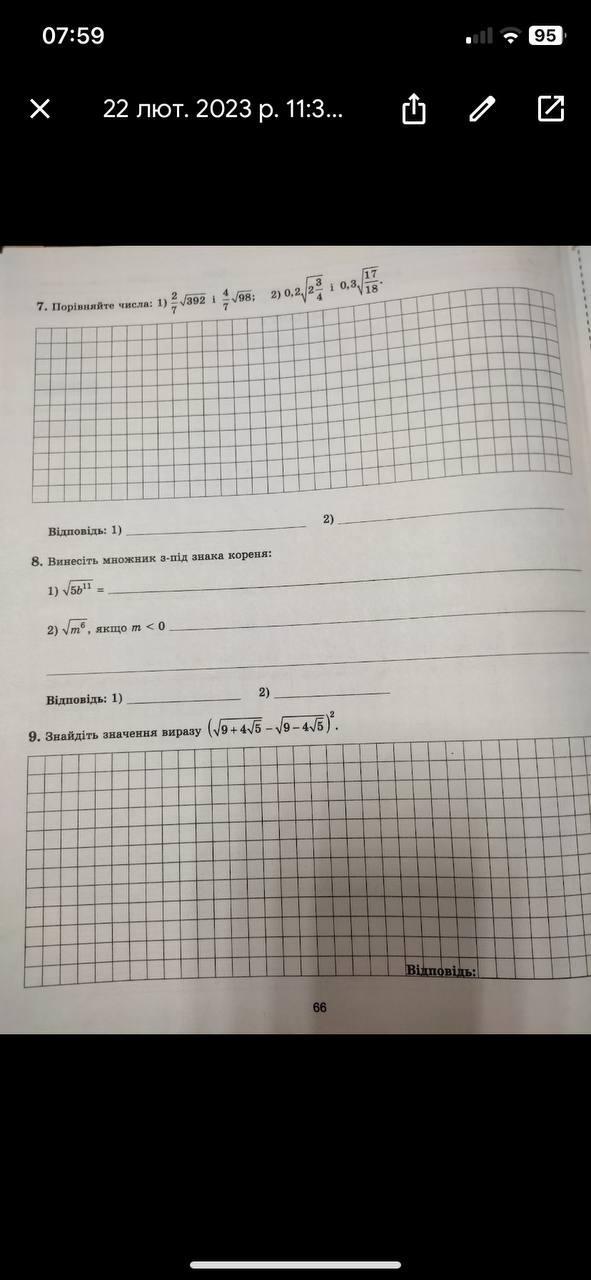
Помгите 7,8 задание прошу
Приложения:
Ответы
Автор ответа:
1
7. 1 Сравнить числа:
и
—————
;
,
Это и ответ.
Или так:
;
,
Это ответ.
7. 2 Сравнить числа:
и
—————
,
;
,
Это ответ.
8. 1 Вынести множитель из под знака корня:
И есть условие, что число под корнем должно быть больше или равно нулю. То есть,
Это ответ.
8. 1 Вынести множитель из под знака корня:
, если
;
Степень (6) — чётная, а если отрицательное число возвести в чётную степень, то число будет положительным. Это удовлетворяет тому условию, что число под корнем должно быть больше или равно нулю.
Это ответ.
Похожие вопросы
Предмет: География,
автор: lugovaanastasa589
Предмет: Українська мова,
автор: senchousnet
Предмет: Литература,
автор: wpohvaliy07
Предмет: Биология,
автор: Oo67
Предмет: География,
автор: olabaturina2005