Предмет: Геометрия,
автор: sviatilutskaadianaa
У трикутнику ABC <A = 45º, <C = 30º, а сторона ВС = √2 см.
Знайти сторону AB
а)√2см; б) √2/2см; б) 1см.
Приложения:
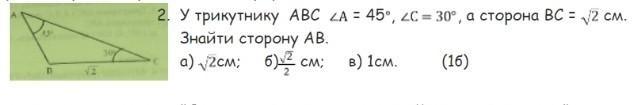
Ответы
Автор ответа:
1
Відповідь:
в) 1 см
Пояснення:
- Сума гострих кутів прямокутного трикутника дорівнює 90°
- Катет прямокутного трикутника, що лежить навпроти кута 30°, дорівнює половині гіпотенузи (гіпотенуза удвічі довша від катета навпроти кута 30°).
- Якщо в трикутнику два кути рівні, то він рівнобедрений.
- Рівнобедрений трикутник - це трикутник, у якого дві сторони рівні між собою.
Розв'язування:
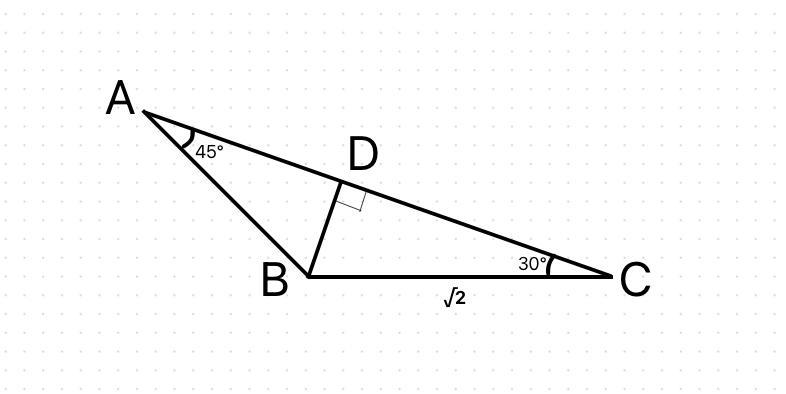
З точки B проведемо висоту BD.
1) Розглянемо прямокутний трикутник BDC(∠BDC=90°)
BD - катет, що лежить навпроти кута ∠C=30°
ВD=BC/2= √2/2 (см) - так як гіпотенуза удвічі довша від катета навпроти кута 30°
2) Розглянемо прямокутний трикутник ABD(∠ADB=90°)
За теоремою про суму гострих кутів прямокутного трикутника, знайдемо ∠АBD:
∠АBD=90°-∠A=90°- 45° = 45°
Отже трикутник ABD рівнобедрений, тому AD = BD = √2/2
Знаходимо за теоремою Піфагора AB
AB^2 = (√2/2)^2 + (√2/2)^2
AB^2 = 4/4
AB = √1 = 1
Відповідь: 1 см
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: Goooooooook
Предмет: Информатика,
автор: kkekk8669
Предмет: Физика,
автор: rphyevnmrsjilgt
Предмет: Английский язык,
автор: stikman002