Предмет: Алгебра,
автор: Muktarovalashyn
всего 4 задания. дам 100ббал.
Срочнаа надоооо))^_^
Приложения:
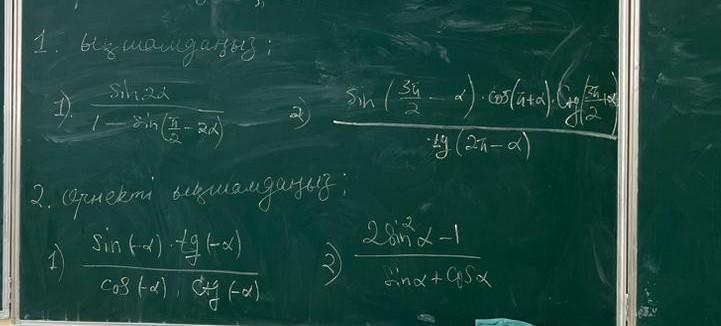
Ответы
Автор ответа:
1
Universalka:
По какой причине отметили нарушение ?
не знаю , случайно было
теперь как отменить
Приветик, не могл(а), бы ты пожайлуста посмотреть , и решить мне новое задание! - спасибо большое, что помогаешь :))
Похожие вопросы
Предмет: Английский язык,
автор: y10715587
Предмет: Физкультура и спорт,
автор: vladaparhomenko234
Предмет: География,
автор: Anfisarat
Предмет: Алгебра,
автор: mimi2006hihihi