Question

Помогите! Срочно!

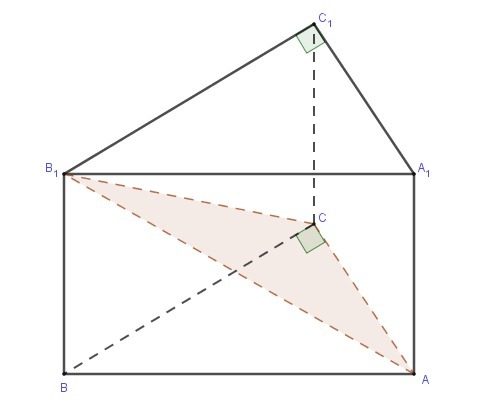
В основании прямой призмы ABCA1B1C1  лежит прямоугольный  треугольник АВС (угол C=90 градусов), AC=4см, BC=3см.
Через сторону AC и вершину B1 проведена плоскость, угол B1AC=60 градусов.
Найдите площадь боковой поверхности призмы.

Answer 1

Из треугольника ABC по т. Пифагора $AB=sqrt{AC^2+BC^2}=5$ см.

Так как BB₁ ⊥ (ABC) и BC ⊥ AC то B₁C ⊥ AC (по теореме о трех перпендикулярах), следовательно, ΔB₁CA - прямоугольный.

∠B₁AC = 60°, тогда ∠AB₁C = 90° - 60° = 30°

Против угла 30° гипотенуза АВ₁ в два раза больше катета АС,т.е.

AB₁ = 2AC = 2 * 4 = 8 см

Из прямоугольного треугольника AB₁B: $BB_1=sqrt{AB_1^2-AB^2}=sqrt{39}$ см

Площадь боковой поверхности призмы:

 Sбок = Pосн * h = (AB+BC+AC)*BB₁ = (5+3+4)*√39 = 12√39 см²

Ответ: 12√39 см²