Предмет: Алгебра,
автор: geo33
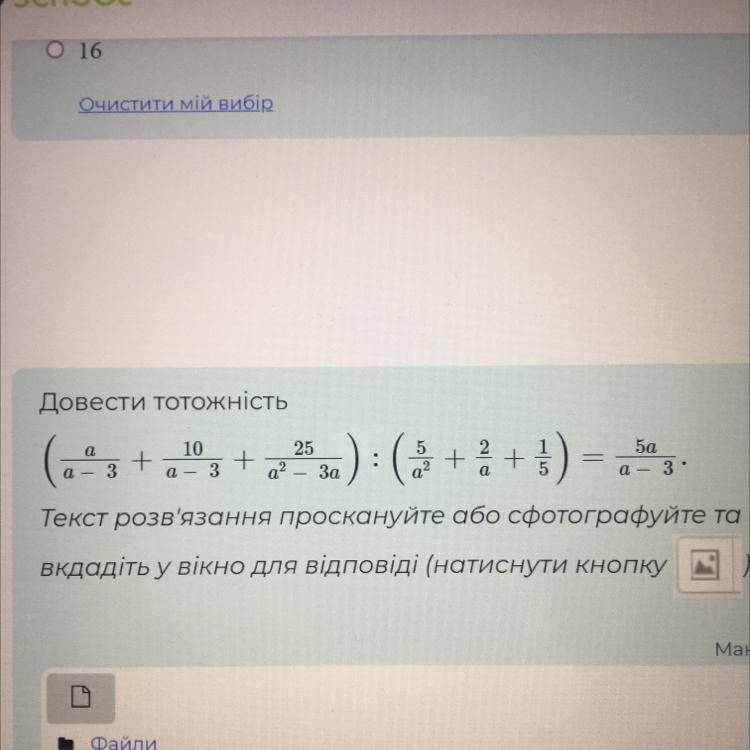
Довести тотожність вираза
Приложения:
Ответы
Автор ответа:
0
Відповідь:
ответ на фото, удачи)
Пояснення:
Приложения:

Автор ответа:
0
Відповідь:
тотожність доведено
Пояснення:
скорочуємо та а
Похожие вопросы
Предмет: Литература,
автор: denisvit319
Предмет: Химия,
автор: a2035578
Предмет: Химия,
автор: a2035578
Предмет: Математика,
автор: sbutkeeva
Предмет: История,
автор: alinazhalilova17