Предмет: Геометрия,
автор: shadeyt146
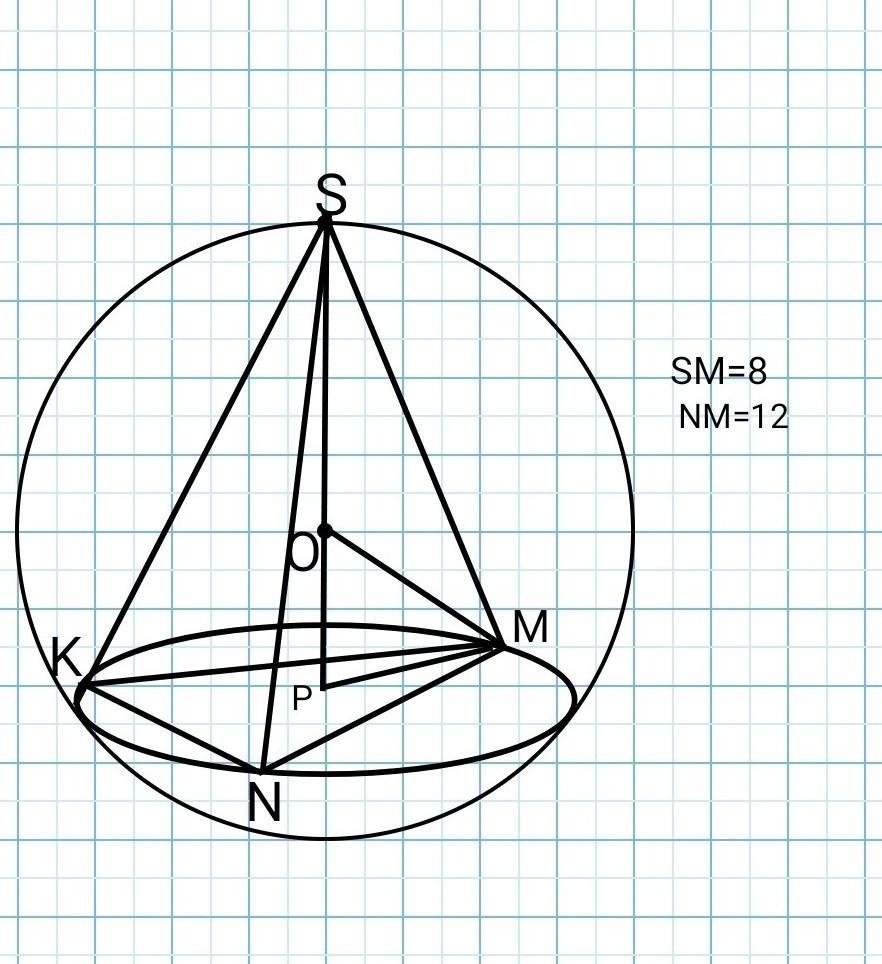
Найдите площадь поверхности шара, описанной вокруг правильной треугольной пирамиды, сторона основания которой равна 12 см, а боковое ребро — 8 см.
Ответы
Автор ответа:
1
Ответ:
Sшар=256π см²
Объяснение:
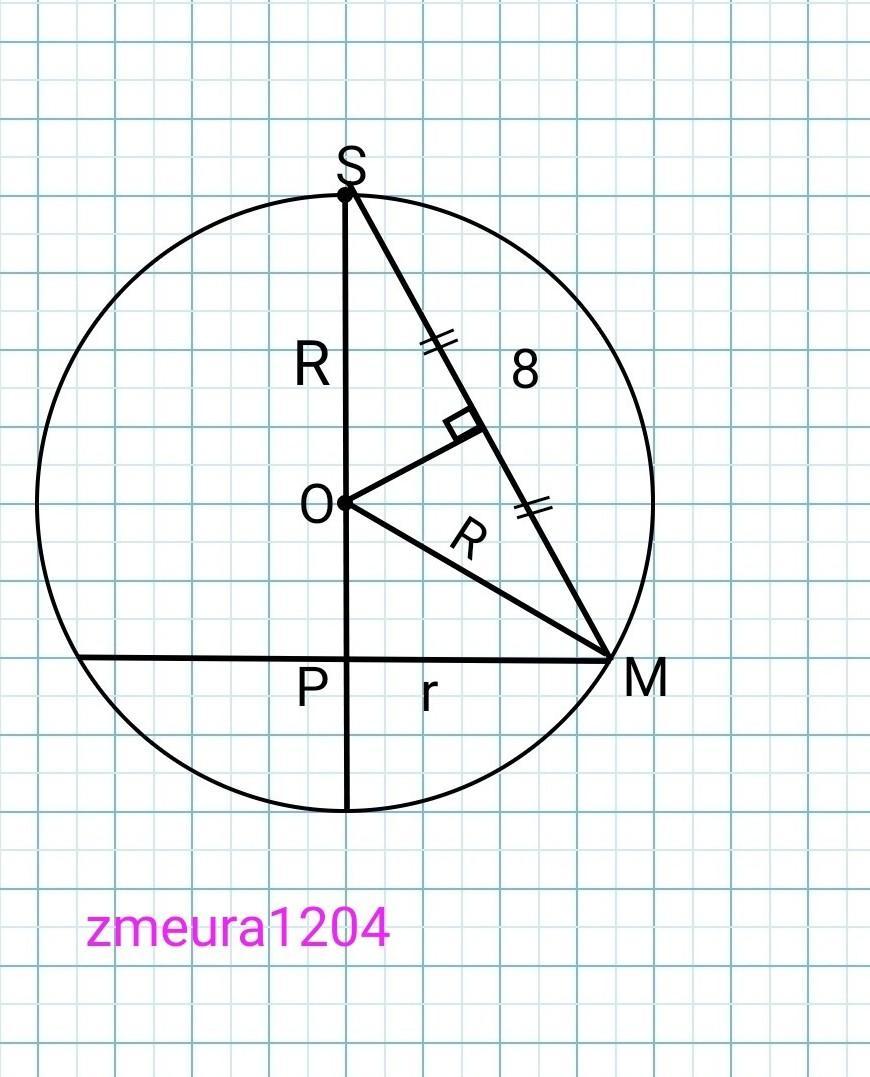
PM=MN/√3=12/√3=4√3 см.
По теореме Пифагора:
SP=√(SM²-PM²)=√(8²-(4√3)²)=4см.
Катет SP в два раза меньше гипотенузы SM, ∠SMP=30°
∠PSM=90°-∠SMP=90°-60°=60°
∆SOM- равнобедренный треугольник SO=OM=R.
С углом 60°, следствие ∆SOM- равносторонний треугольник. SO=OM=SM=8см
Sшар=4πR²=8²*4π=256π см²
Приложения:
Похожие вопросы
Предмет: Право,
автор: bogdanovabogdana2020
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: kozahmetovakamila45
Предмет: Химия,
автор: brinyuk1234
Предмет: Русский язык,
автор: Profomaster