Предмет: Алгебра,
автор: kirilukmaria88
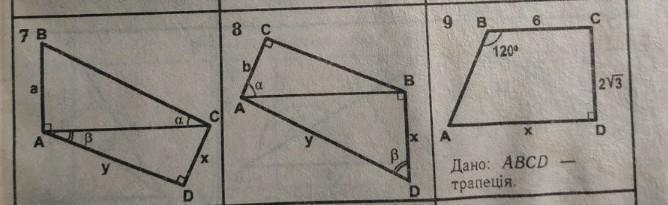
розв'язання прямокутних трикутників знайти х та у
завдання 7, 8, 9
Приложения:
Ответы
Автор ответа:
2
№7
В ΔАВС : АС=а*ctgα
В ΔАDС : DC= x=AC*sinβ=а*ctgα*sinβ
AD=y=AC*cosβ=АС=а*ctgα*cosβ
№8
В ΔАВС : АВ=b/cosα;
В ΔАBD : AD= y=AB/sinβ=b/(cosα*sinβ);
BD=х=АD*cosβ=bcosβ/(cosα*sinβ)=b*ctgβ/cosα
№9
Проведем высоту из вершины В к стороне АD, пусть точка пересечения высоты ТВ и стороны АD - точка Т. Тогда в треугольнике АТВ : ∠В=120°-90°=30°, и против этого угла лежит катет АТ, равный половине гипотенузы АВ, тогда, если АТ=х, АВ=2х, ВТ=СD=2√3; по теореме Пифагора для ΔАВТ: 4х²-х²=(2√3)², откуда 3х²=4*3, х>0, х²=4, поэтому х=2, значит, х=АD=AT+TD=AT+BC=2+6=8
kirilukmaria88:
спасибо большое за помощь
Похожие вопросы
Предмет: Другие предметы,
автор: supergril
Предмет: Математика,
автор: vpv20120104
Предмет: Українська література,
автор: Alisaa5600
Предмет: Алгебра,
автор: hehdhfh
Предмет: Математика,
автор: Аноним