Предмет: Алгебра,
автор: ila228212
ПРОШУ ПОМОГИТЕ! ЗАДАНИЕ НА КАРТИНКЕ
Приложения:
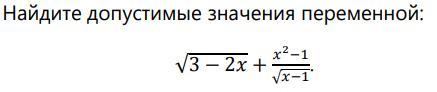
Ответы
Автор ответа:
1
Подкоренное выражение корня чётной степени должно быть неотрицательным , то есть ≥ 0 , но если этот корень в знаменателе , то подкоренное выражение должно быть строго больше нуля , так как на ноль делить нельзя .
ila228212:
спасибо большое!!
Похожие вопросы
Предмет: История,
автор: chepelievata
Предмет: Английский язык,
автор: sofiaklimenko1405
Предмет: Химия,
автор: al2008lexa
Предмет: Қазақ тiлi,
автор: aitbaikundukpaev