Предмет: Алгебра,
автор: Alexxx0013
Помогите пожалуйста решить задачу
Приложения:
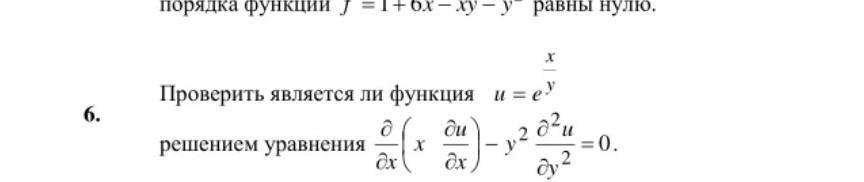
Ответы
Автор ответа:
1
Решение.
Вычислим частные производные .
Подставим найденные выражения в функцию .
Заданная функция не является решением уравнения .
Приложения:


Alexxx0013:
спасибо огромное
вы лучший
еше вопрос без ответа осталось
Похожие вопросы
Предмет: История,
автор: uppihouse
Предмет: Английский язык,
автор: ganerkan82
Предмет: Українська література,
автор: nastademesko249
Предмет: Русский язык,
автор: kuzyansk13
Предмет: Математика,
автор: eneta