Завдання на фото!!! Дано і розписать, малюнок


Ответы
Объяснение:
400)
Дано:
ABCD - квадрат.
т.О- перетину діагоналей.
МО перпендикулярно (АВС)
МК перпендикулярно СD
МО=8см
MK=10см
S(ABCD)=?
Розв'язання:
∆МОК- прямокутний трикутник.
За теоремою Піфагора:
ОК=√(МК²-МО²)=√(10²-8²)=6см
АD=2*OK=2*6=12см
S(ABCD)=AD²=12²=144см²
Відповідь: 144см²
__________________
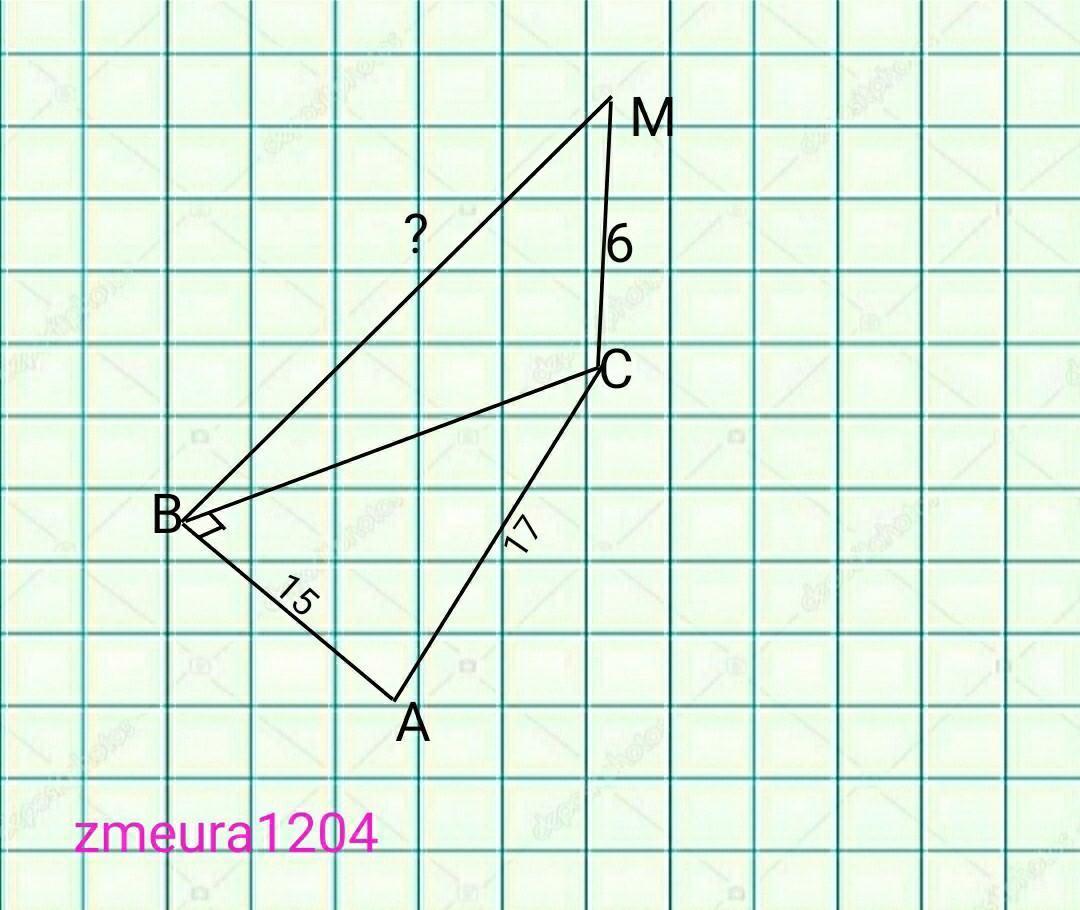
396)а)
Дано:
∆АВС- прямокутний трикутник.
∠В=90°
МС перпендикулярно (АВС)
АС=17см
ВА=15см
МС=6см
МВ=?
Розв'язання:
∆АВС- прямокутний трикутник.
За теоремою Піфагора:
ВС=√(АС²-АВ²)=√(17²-15²)=√(289-225)=
=√64=8см.
∆МСВ- прямокутний трикутник.
За теоремою Піфагора:
МВ=√(МС²+ВС²)=√(6²+8²)=10см
Відповідь: 10см
__________________
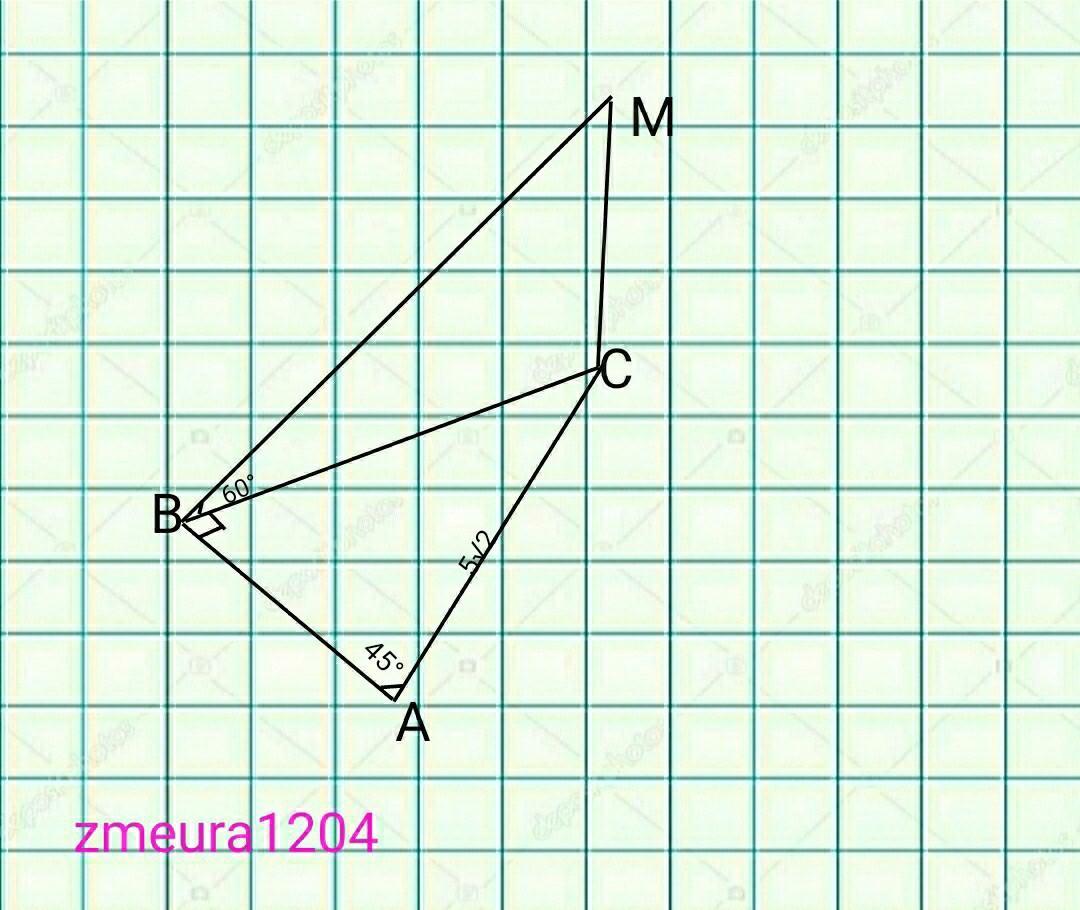
396б)
Дано:
∆АВС- прямокутний трикутник.
∠В=90°
АС=5√2см
∠А=45°
МО перпендикулярно (АВС)
∠МВС=60°
МВ=?
Розв'язання:
∆АВС- прямокутний, рівнобедрений трикутник. Кути при основі рівні 45°.
АВ=ВС;
ВС=АС/√2=5√2/√2=5см.
∆МВС- прямокутний трикутник.
Сума гострих кутів прямокутного трикутника дорівнює 90°
∠ВМС=90°-∠МВС=90°-60°=30°
ВС- катет проти кута 30°
МВ=2*ВС=2*5=10см
Відповідь: МВ=10см