Предмет: Алгебра,
автор: xzchinaaa
звільнитися від ірраціональності в знаменнику



Ответы
Автор ответа:
1
Ответ:
вот решение
Объяснение:
решение нижн
Приложения:
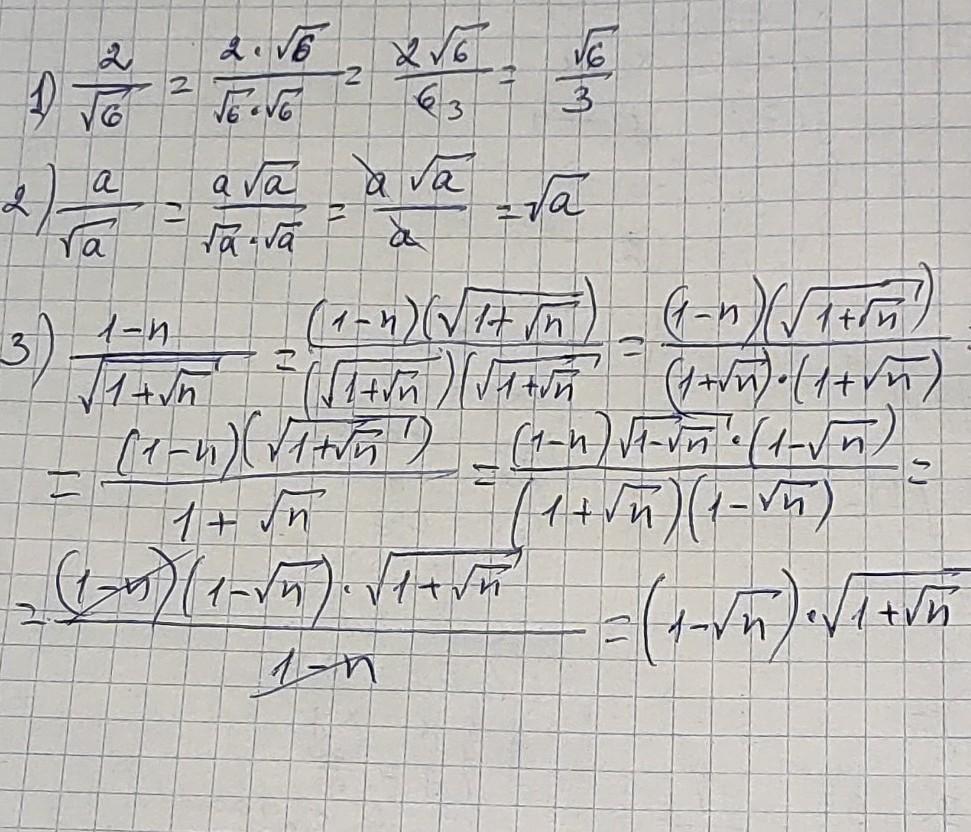
Автор ответа:
0
henwnwnsjsnsns:
Добрый день! Не могли бы вы мне помочь, пожалуйста? https://znanija.com/task/51970602
Похожие вопросы
Предмет: Математика,
автор: D110
Предмет: Алгебра,
автор: uro1rvhx
Предмет: Українська мова,
автор: ikalchenko23
Предмет: Английский язык,
автор: nihatibrahimovfnen80
Предмет: Литература,
автор: omiroslava191