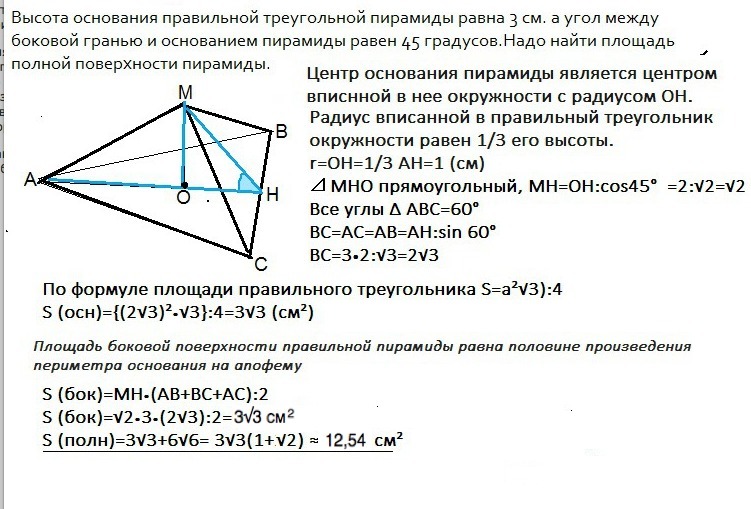
Высота основания правильной треугольной пирамиды равна 3 см. а угол между боковой гранью и основанием пирамиды равен 45 градусов.Надо найти площадь полной поверхности пирамиды Если можно, то вместе с рисунком пожалуйста.
Ответы
Высота основания правильной треугольной пирамиды равна 3 см. а угол между боковой гранью и основанием пирамиды равен 45°.
Найти площадь полной поверхности пирамиды.
Площадь полной поверхности равна сумме площади основания и площади боковой поверхности.
Для решения нужно знать сторону основания и апофему ( высоту боковой грани).
См. рисунок, данный в приложении.
По условию АН=3 см,∠МНО=45°
Центр основания пирамиды является центром вписанной в него окружности с радиусом ОН.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты.
r=ОН=1/3 АН=1 (см)
⊿ МНО прямоугольный, МH=OH:cos45°=2:√2=√2
Все углы ∆ АВС=60°
ВС=АС=АВ=АН:sin 60°
BC=3•2:√3=2√3
По формуле площади правильного треугольника S=a²√3):4
S (осн)={(2√3)²•√3}:4=3√3 (см²)
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
S (бок)=МН•(АВ+ВС+АС):2
S (бок)=√2•3•(2√3):2=3√6 (см²)
S (полн)=3√3+3√6= 3√3(1+√2) ≈12,54 см²