Вычислите tg (п/6 +а), если cosa= -0,8 и п< a < 3п/2. Какой четверти принадлежит угол п/6 + а?
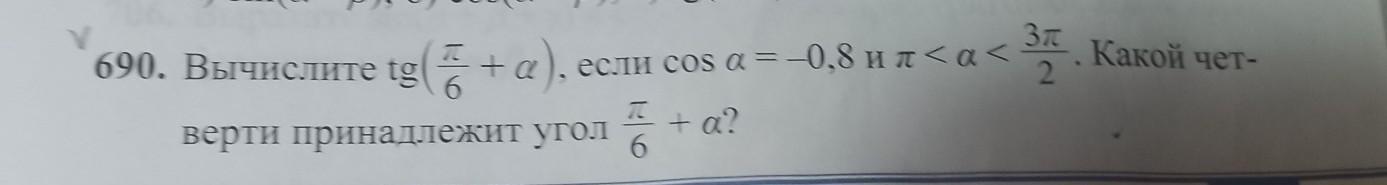
Ответы
Ответ:
Довжина дошки: 1,8 м. (Dovzhyna doshky: 1,8 m.)
Piptik
Дошку завдовжки 7,2 м розрізали на чотири рiвнi частини. Знайди довжину однієï частини дошки.
Для знаходження довжини однієї частини дошки, необхідно довжину всієї дошки (7,2 м) розділити на кількість частин, на які її розрізали, тобто на 4:
7,2 м / 4 = 1,8 м
Отже, довжина однієї частини дошки дорівнює 1,8 м.
Piptik
(x-5)(x-3)=0
Розв'язуємо рівняння:
(x-5)(x-3)=0
Застосовуємо властивість множення: добуток двох множників дорівнює нулю тоді і тільки тоді, коли хоча б один з множників дорівнює нулю.
Отже, маємо два рівняння:
x-5=0 або x-3=0
Розв'язуємо кожне з них:
x-5=0 --> x=5
x-3=0 --> x=3
Отже, розв'язки рівняння: x=5 або x=3.
Piptik
Вычислите tg (п/6 +а), если cosa= -0,8 и п< a < 3п/2. Какой четверти принадлежит угол п/6 + а?
Застосуємо формулу для тангенсу суми кутів:
tg(п/6 + а) = (tg(п/6) + tg(а)) / (1 - tg(п/6) * tg(а))
Так як п/6 = 30 градусів, то tg(п/6) = tg(30 градусів) = 1/√3.
Оскільки cos(a) = -0,8, то знайдемо sin(a) за формулою sin^2(a) + cos^2(a) = 1:
sin(a) = √(1 - cos^2(a)) = √(1 - 0,8^2) = √0,36 = 0,6.
Тоді tg(a) = sin(a) / cos(a) = 0,6 / (-0,8) = -0,75.
Підставляємо в формулу для tg(п/6 + а):
tg(п/6 + а) = (1/√3 - 0,75) / (1 - (1/√3) * (-0,75)) = (1/√3 - 0,75) / (1 + 0,75/√3) = (1 - 0,75√3) / (√3 + 3/4).
Объяснение: