Question

исследовать функцию!
 х3 - 3х

Answer 1

1. Область определения функции: множество всех действительных чисел

2. f(-x) = - x³ + 3x = - (x³ - 3x) = - f(x) - нечетная функция

3. Непериодическая.

4. Точки пересечения с осью Ох и Оу.

f(x) = 0;  x³ - 3x = 0;   x(x²-3)=0

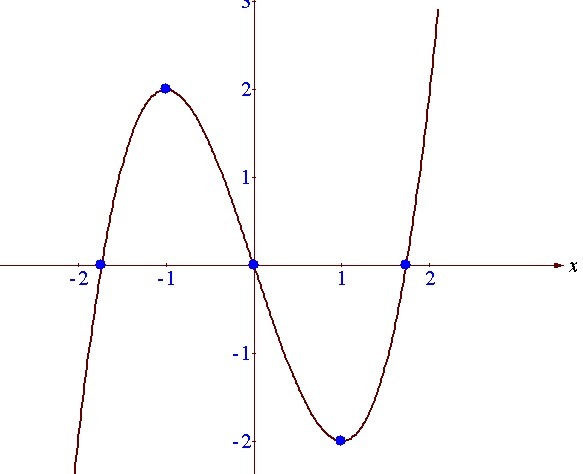
(0;0), (-√3;0), (√3;0) - точки пересечения с осью Ох

x=0; f(x)=0;  (0;0) - с осью Оу.

5. Монотонность функции

f'(x) = (x³ - 3x)' = 3x² - 3 = 0

x² - 1 = 0

x = ±1

___+___(-1)___-__(1)__+___
Функция возрастает на промежутке x ∈ (-∞;-1) и x ∈ (1;+∞), а убывает - x ∈ (-1;1). x=-1 - локальный максимум. х=1 - локальный минимум.

7. Точки перегиба
f''(x) = 6x = 0  откуда х=0

Горизонтальных, наклонных и вертикальных асимптот нет.