Предмет: Алгебра,
автор: Аноним
помогите пожалуйста с алгеброй все а.б.в.г
Приложения:
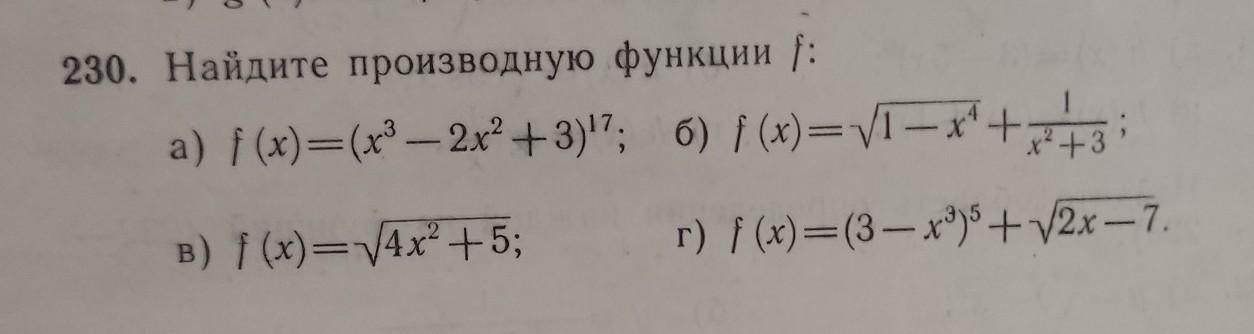
elzes:
попробуй приложение Photomath. Там подробно и понятно, но обычно работает только с алгеброй(с геометрией не очень)
Ответы
Автор ответа:
1
Ответ:
Объяснение:
a) f(x)=
f'(x) =17*(
b) f(x) =
f'(x) = -4x³ /(2*
c) f(x)=
d) f(x)=
Автор ответа:
1
Объяснение:
a)
б)
в)
г)
В б) под корнем x^4 , в решении х^1
Посмотрите как у меня. У меня все правильно.
Cпасибо за подсказку, я исправил.
Спасибо за подсказку. я исправил.
Похожие вопросы
Предмет: География,
автор: Demon1234Angel
Предмет: История,
автор: angelinastarinaf
Предмет: Химия,
автор: evgenijomelanov
Предмет: Другие предметы,
автор: Yyyuuufyy
Предмет: Математика,
автор: Fox5050