Предмет: Алгебра,
автор: Аноним
Помогите помогите пожалуйста, кто нибудь, сегодня уже надо сдавать
Приложения:
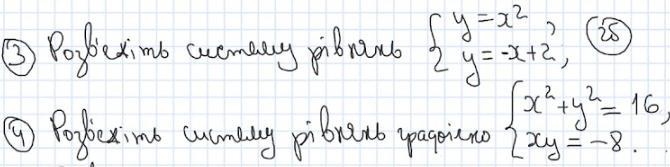
Ответы
Автор ответа:
1
Ответ:
Решаем системы методом подстановки . Из одного уравнения выражаем одну из переменных и подставляем найденное значение во второе уравнение .
NNNLLL54:
да, корни квадр. уравнения находим по теореме Виета .
Похожие вопросы
Предмет: История,
автор: aleksandracajkina463
Предмет: Українська мова,
автор: foxiniks5
Предмет: Физика,
автор: nalyvaikodaria
Предмет: Русский язык,
автор: macande