Знайдіть площу фігури, обмеженої лініями
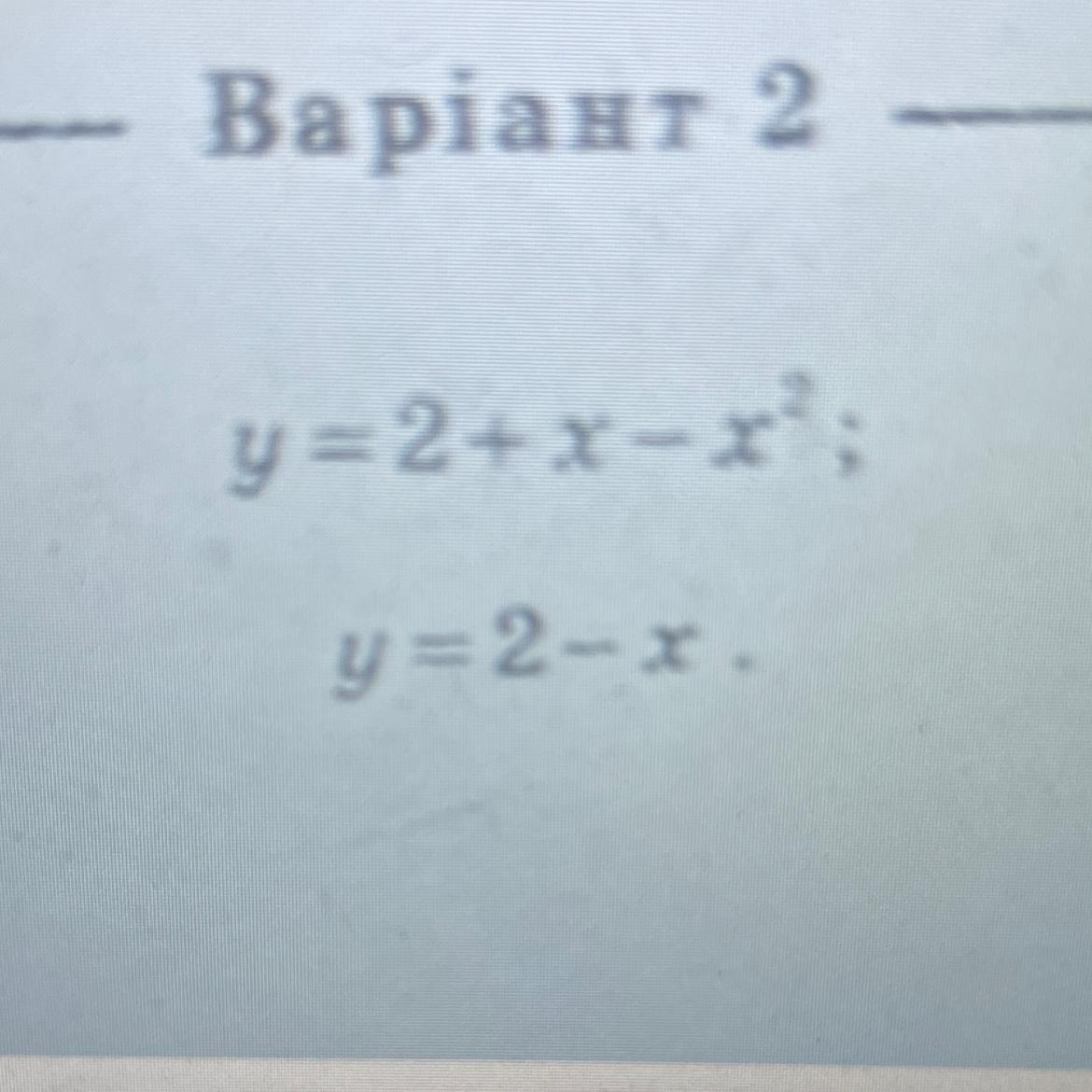
Ответы
Ответ:
площа фігури, обмеженої лініями y = 2 + x - x² та y = 2 - x, дорівнює 4/3. Можете сделать мой ответ лучшим??
Объяснение:
Спочатку необхідно знайти точки перетину цих двох ліній, розв'язавши систему рівнянь:
2 + x - x² = 2 - x
Після спрощення отримаємо рівняння квадратного виду:
x² + 2x = 0
x(x + 2) = 0
x = 0 або x = -2.
Підставляючи ці значення x у рівняння y = 2 + x - x² та y = 2 - x, отримуємо відповідні значення y:
для x = 0: y = 2 + 0 - 0² = 2, y = 2 - 0 = 2;
для x = -2: y = 2 - 2 + 4 = 4, y = 2 + 2 = 4.
Таким чином, точки перетину цих ліній - це (0, 2) та (-2, 4).
Далі, щоб знайти площу фігури, обмеженої цими лініями, необхідно знайти інтеграл від різниці між функціями y = 2 + x - x² та y = 2 - x за межами відповідних інтервалів x:
S = ∫[-2,0] (2 + x - x² - (2 - x)) dx
S = ∫[-2,0] (2x - x²) dx
S = [x² - (1/3)x³] [-2,0]
S = (0 - 0) - ((4/3) - (8/3))
S = 4/3.
Отже, площа фігури, обмеженої лініями y = 2 + x - x² та y = 2 - x, дорівнює 4/3.