Предмет: Алгебра,
автор: dd9783232
Доведіть,що значення виразу ділиться на 25
2^12+3^6
Ответы
Автор ответа:
1
Розв'язання:
Розв'язання у вкладеному файлі.
Пояснення:
Думаю, очевидно, що будь-який алгебраїчний вираз треба спростити (якщо це можливо) або привести до певного вигляду, перш ніж щось робити. Нам треба довести, що його значення ділиться націло на 25. Найчастіше у таких завданнях ми показуємо, що один з множників дорівнює тому чи іншому числу. Спробуємо привести 2^12+3^6 до вигляду 25(...).
Подамо у вигляді
Тут уже зрозуміліше, бо у нас є хоча б спільний показник степеня. Використовуючи формулу розкладання на множники многочленів виду a^n + b^n (де n - непарне натуральне число), отримаємо:
Далі проста арифметика. Значення дорівнює 25. По суті уже не має сенсу знаходити значення виразу в правій дужці, бо головне ми показали.
Приложения:
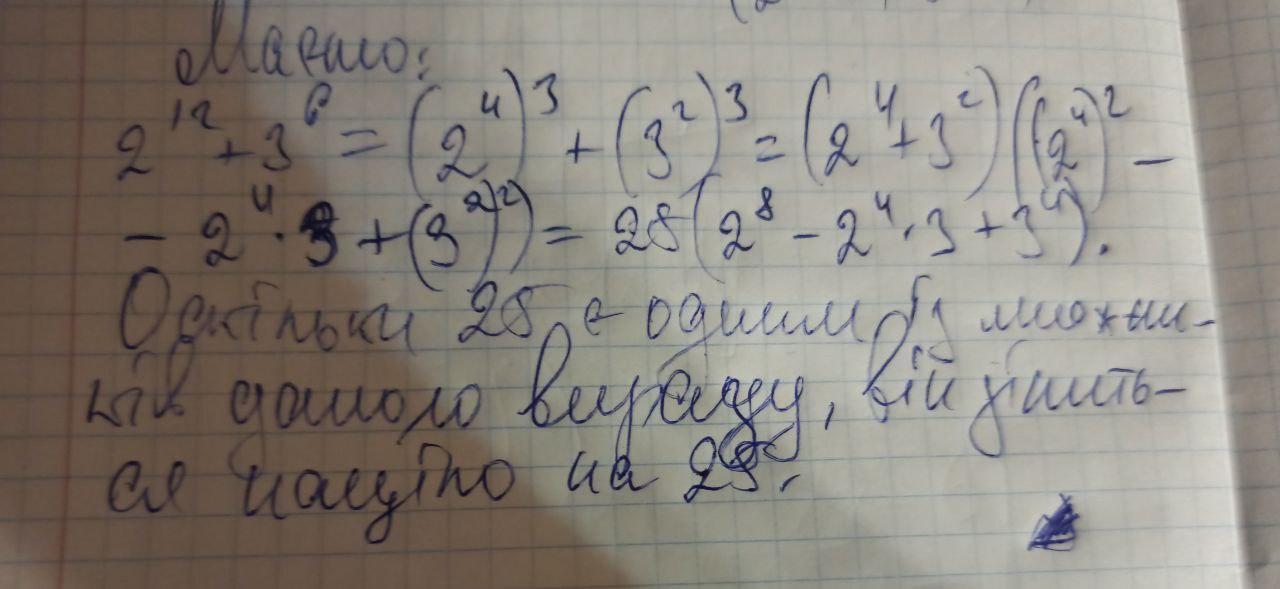
Похожие вопросы
Предмет: Русский язык,
автор: sulaimanovemir2
Предмет: Геометрия,
автор: shirina116
Предмет: Русский язык,
автор: jypar270191
Предмет: Математика,
автор: kausarorazbek09
Предмет: Английский язык,
автор: aylinakhusnullina