Предмет: Геометрия,
автор: yarikudovichenko
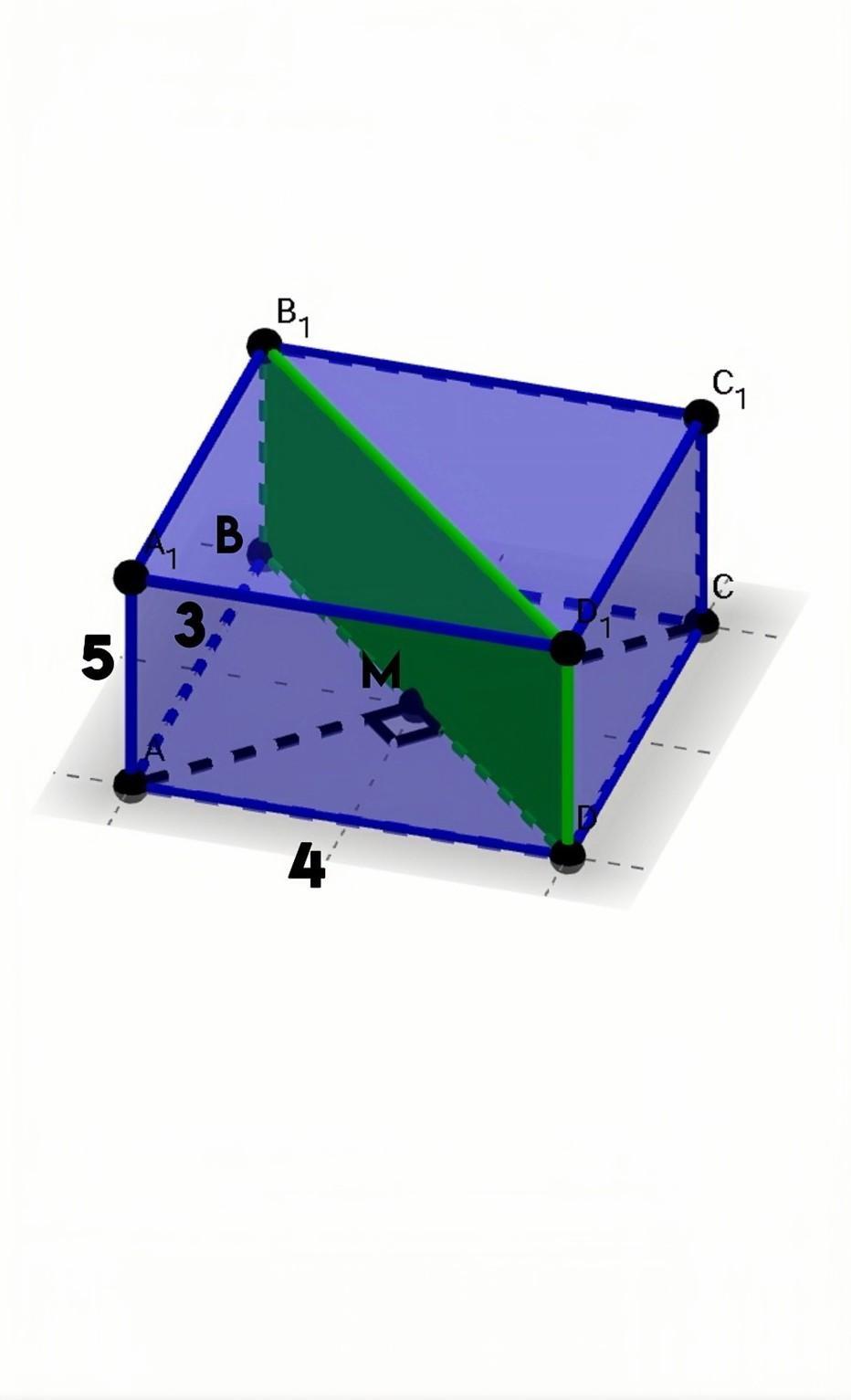
ABCDA1B1C1D1 - прямокутний паралелепіпед. АВ = 3 см, АD = 4 см, АА1= 5 см. Чому дорівнює відстань від точки А до площини (BDD1)?
Ответы
Автор ответа:
9
Ответ:
Р(А;(BDD₁)) = 2,5см
Объяснение:
ПЕРЕВОД: ABCDA1B1C1D1 – прямоугольный параллелепипед. АВ = 3 см, АD = 4 см, АА1 = 5 см. Чему равно расстояние от точки А до плоскости (BDD1)?
-----------------------------------------------------------
Дано: ABCDA₁B₁C₁D₁ – прямоугольный параллелепипед, АВ = 3 см, АD = 4 см, АА₁ = 5 см
Найти: Р(А;(BDD₁))
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Расстояние от точки до плоскости - это перпендикуляр, опущенный из данной точки на плоскость. Р(А;(BDD₁)) = АМ, то есть половина диагонали АС.
- Т.к. это прямоугольный параллелепипед, то все грани - прямоугольники. Диагональ АС согласно Т.Пифагора равна:
⠀⠀⠀ АС = √(AD²+CD²)
⠀⠀⠀AC = √(4²+3²)
⠀⠀⠀AC = √(16+9)
⠀⠀⠀AC = √25 = 5см.
- Диагонали прямоугольника точкой пересечения делятся попалам, тогда АМ = 2,5см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: mamamamadova
Предмет: Литература,
автор: schiry2015
Предмет: Українська мова,
автор: htmw5xtxw8
Предмет: Физика,
автор: goolefinh333
Предмет: Английский язык,
автор: danatatu49