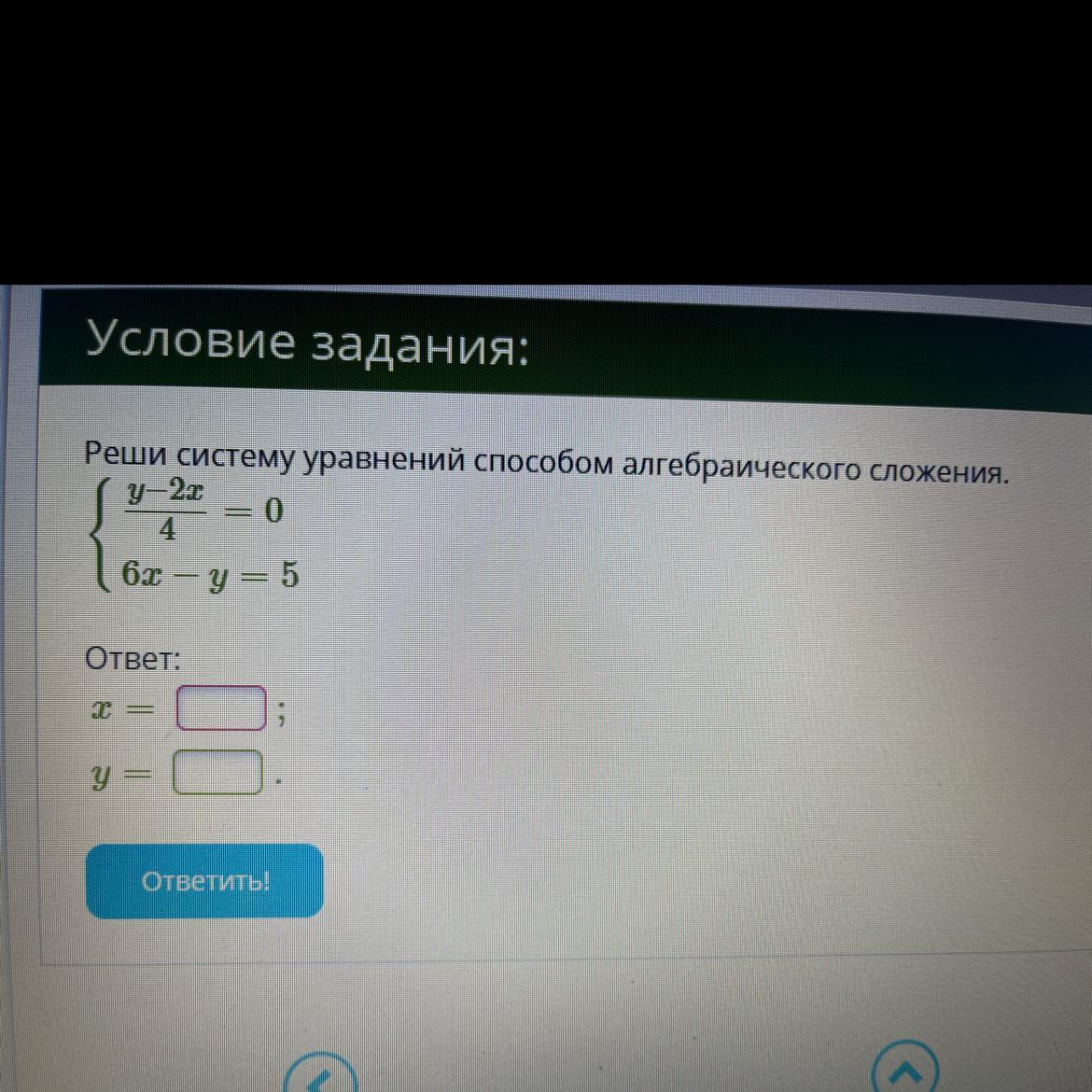
Реши систему уравнений способом алгебраического сложения.
y-2x
= 0
4
6x - у - 5
Ответ:
X =
y=
ОО
Ответы
Для решения системы уравнений методом алгебраического сложения нужно выразить одну из переменных через другую в одном из уравнений и подставить это выражение в другое уравнение, после чего решить получившееся уравнение от одной переменной и найти значение другой.
В данной системе уравнений удобно выразить y из первого уравнения:
y - 2x/4 = 0
y = 2x/4
y = x/2
Подставляем это выражение во второе уравнение:
6x - (x/2) - 5 = 0
Упрощаем:
12x - x - 20 = 0
11x = 20
x = 20/11
Теперь можем найти значение y, подставив найденное значение x в любое из уравнений:
y = x/2 = (20/11)/2 = 10/11
Итак, решение системы уравнений:
x = 20/11
y = 10/11
Метод алгебраического сложения:
- Уравнять модули коэффициентов при одном из неизвестных.
- Сложить или вычесть уравнения.
- Решить полученное уравнение с одной переменной.
- Подставить поочерёдно каждый из найденных на третьем шаге корней уравнения в одно из уравнений исходной системы, найти второе неизвестное
чтобы выровнять коэффициенты при неизвестном у, умножим 1 уравнение на 4. Получим:
сложив оба уравнения получим:
у - 2х + 6х - у = 0 + 5
приведем подобные:
4х = 5
х = 1,25
подставим полученный х во 2 уравнение:
6*1,25 - у = 5
у = 7,5 - 5
у = 2,5
Ответ: х = 1,25; у = 2,5