Question

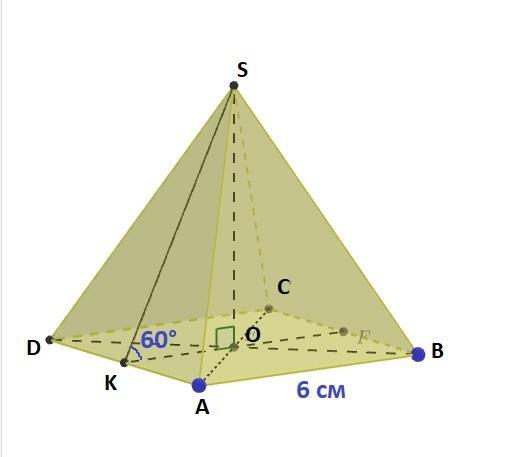
Сторона основи правильної чотирикутної піраміди дорівнює 6 см, усі її бічні грані нахилені до площини основи під кутом 60. Визначте площу бічної поверхні цієї піраміди.​

Answer 1

Ответ:

Площа бічної поверхні піраміди дорівнює 72 см²

Объяснение:

Сторона основи правильної чотирикутної піраміди дорівнює 6 см, усі її бічні грані нахилені до площини основи під кутом 60. Визначте площу бічної поверхні цієї піраміди.

Нехай SABCD - дана правильна чотирикутна піраміда, ABCD - квадрат зі стороною 6 см, SK - апофема. К - середина відрізка AD. Трикутники OAD і SAD-рівнобедрені ⇒ медіани OК і SК є також і висотами.

SK⊥AD, ОК⊥AD ⇒ (SOK)⊥AD

∠SKO = 60° - лінійний кут відповідного двограного кута між площинами (SAD) i (ABC).

1 варіант

Розглянемо прямокутний ΔSOK(∠SOK=90°)

ОК = 1/2 · АВ = 3 (см)

За означенням косинуса гострого кута прямокутного трикутника знайдемо гіпотенузу SК – апофему піраміди:

$cos\angle SKO=\dfrac{OK}{SK}$

$SK=\dfrac{OK}{cos 60^\circ} =\dfrac{3}{\frac{1}{2} } =\bf 6$  (cм)

Бічну поверхню піраміди знайдемо за формулою:

Sбічн = 1/2 · Росн · SК

де Росн - периметр основи

Росн = 4 · 6 = 24 (см)

Sбічн = 1/2 · 24 · 6 = 72 (см²)

2 варіант

Знайдемо площу основи.

Sосн = АВ² = 6² = 36 (см²).

Так як всі грані піраміди нахилені під однаковим кутом, то основа є ортогональною проекцією бічної поверхні з кутом нахилу 60°.

• Площа ортогональної проекції многокутника на площину дорівнює добутку його площі на косинус кута між площиною многокутника і площиною проекції.

Тоді:

Sбічн = Sосн : cos60° = 36 : 0,5 = 72 (см²).

#SPJ1