Question

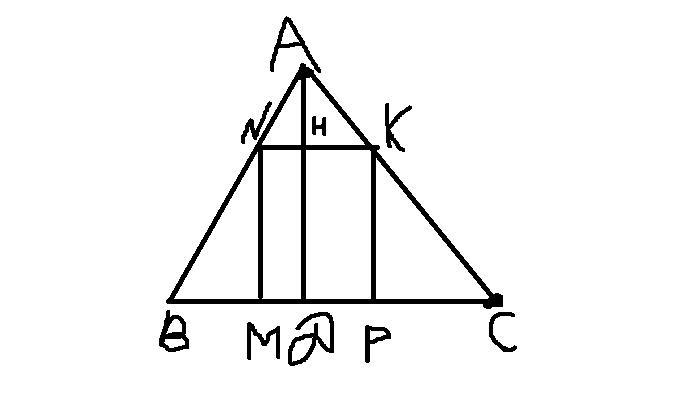
У трикутнику ABC BC=72 см, АД - висота, АД=24 см. У цей трикутник вписано прямокутник MNKP так, що вершини Мі Р належать стороні ВС, а вершини N і К - сторонам АB і AC відповідно. Знайдіть сторони прямокутнику, якщо |MP:MN=9:5.​

Answer 1

Ответ:

Дано:

△NAK

AD=24cм

MNKP(прямокутник)

M і P лежать на стороні BC

N і K(вершини)

Лежить на сторонах AB і AC

|MP:MN=9:5.​

                                                   Розв'язання  

1)MP:72=(24-MN):24 U MP:MN=9:5

NK=MP,MN=KP,DC=72,AD=24,MP:MN=9:5

NK:BC=AH:AD  

HD=MN      

2)AH=24(HD)

MP=1,8MN

3)1,8MN:72=(24MN):24

0,6MN=24(MN)

1,6MN=24

MN=15

MP=1,8⋅15=27

Відповідь:

MN=15

MP=27

Объяснение: