Question

знайти сторону правильного трикутника, описаного навколо кола, якщо сторона правильного чотирикутника, вписаного в це коло дорівнює 8 см​

Answer 1

Ответ:

Сторона правильного трикутника дорівнює 8√6 см

Объяснение:

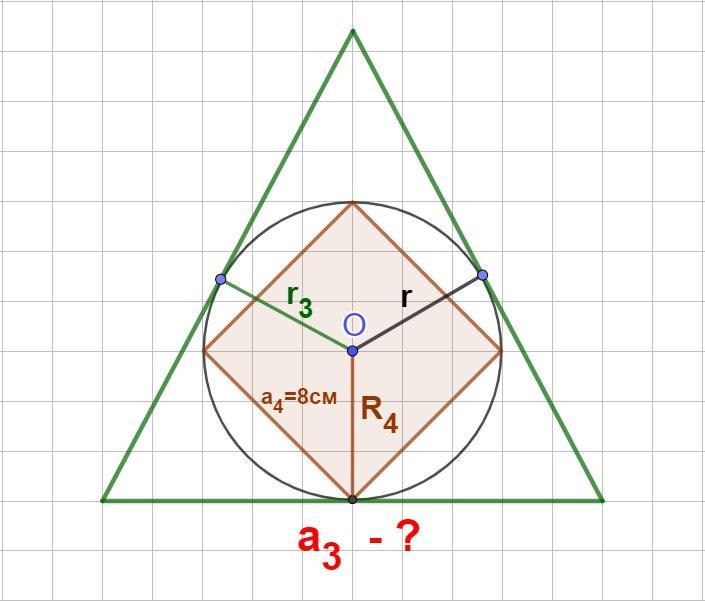
Знайти сторону правильного трикутника, описаного навколо кола, якщо сторона правильного чотирикутника, вписаного в це коло дорівнює 8 см.

Радіус описаного кола навколо правильного чотирикутника:

$\boxed{\bf R_4=\dfrac{a_4\sqrt{2} }{2} }$

Радіус вписаного кола в правильний трикутник:

$\boxed{\bf r_3=\dfrac{a_3\sqrt{3} }{6} }$

Нехай дано коло з центром в точці О, радіуса r. ​Тоді для правильного чотирикутника це буде радіус описаного кола R₄, а для правильного трикутника - радіус вписаного кола r₃. За умовою сторона  правильного чотирикутника, вписаного в це коло:  а₄=8 см.

Отже:

$\sf R_4=\dfrac{a_4\sqrt{2} }{2} =\dfrac{8\sqrt{2} }{2}=4\sqrt{2}$ (см)

Оскількі r₃=R₄, то:

$\sf a_3=2\sqrt{3}\cdot r_3=2\sqrt{3}\cdot R_4=2\sqrt{3}\cdot 4\sqrt{2} =\bf 8\sqrt{6}$  (см)

Відповідь: а₃=8√6 см

#SPJ1