Предмет: Геометрия,
автор: medina270409
Помогите пожалуйста, даю 70 баллов
Приложения:
Ответы
Автор ответа:
2
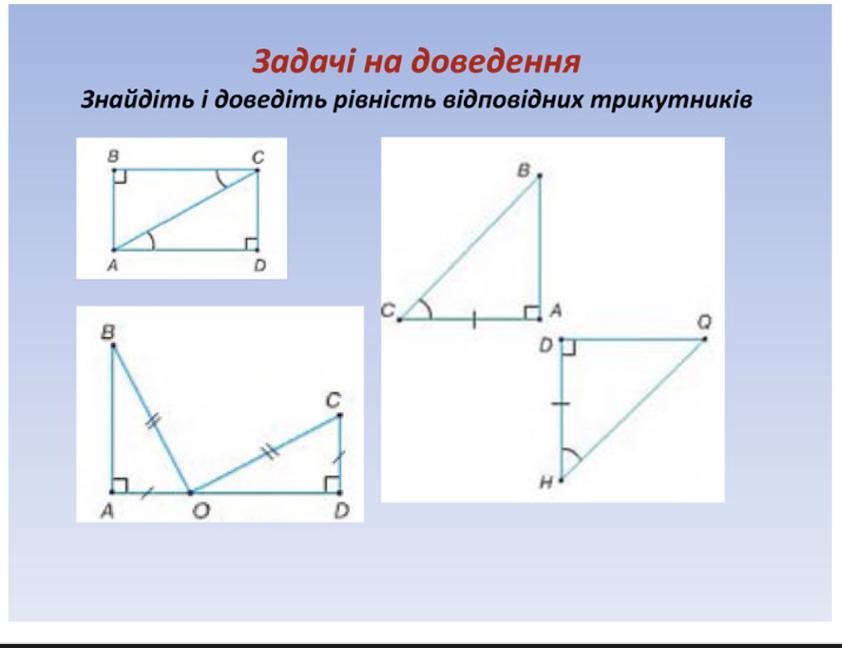
Рассмотрим первый рисунок. Дан прямоугольник АВСD, где диагональ АС делит его на 2 прямоугольных треугольника, ∆АВС и ∆CDА. Докажем, что они равны.
- По условию, ∠САD и ∠ACB равны, потому что при параллельных прямых ВС и AD, и секущей АС они как внутренние накрест лежащие. АС - общая. Тогда по 3-му признаку равенства прямоугольных треугольников(по гипотенузе и острому углу) ⇒ ∆АВС = ∆CDА.
Рассмотрим второй рисунок. Дана ломаная, в которой присутствуют 2 прямоугольных треугольника, ∆АВО и ∆DOС. Докажем, что они равны.
- По условию, у этих треугольников равны гипотенузы ОС и ОВ, равны катеты CD и AO. Тогда по 4-му признаку равенства прямоугольных треугольников(по гипотенузе и катету) ⇒∆АВО = ∆DOС.
Рассмотрим последний рисунок. Даны 2 прямоугольных треугольника, ∆АВС и ∆DQH. Докажем, что они равны.
- По условию, катеты АС и HD равны, ∠АСВ = ∠DHQ. Тогда по 2-му признаку равенства прямоугольных треугольников(по катету и прилежащему острому углу) ⇒ ∆АВС = ∆DHQ.
#SPJ1
Похожие вопросы
Предмет: Биология,
автор: wertyprozzx
Предмет: Английский язык,
автор: r9872446
Предмет: Физика,
автор: maria1365
Предмет: Физика,
автор: gems111555