Question

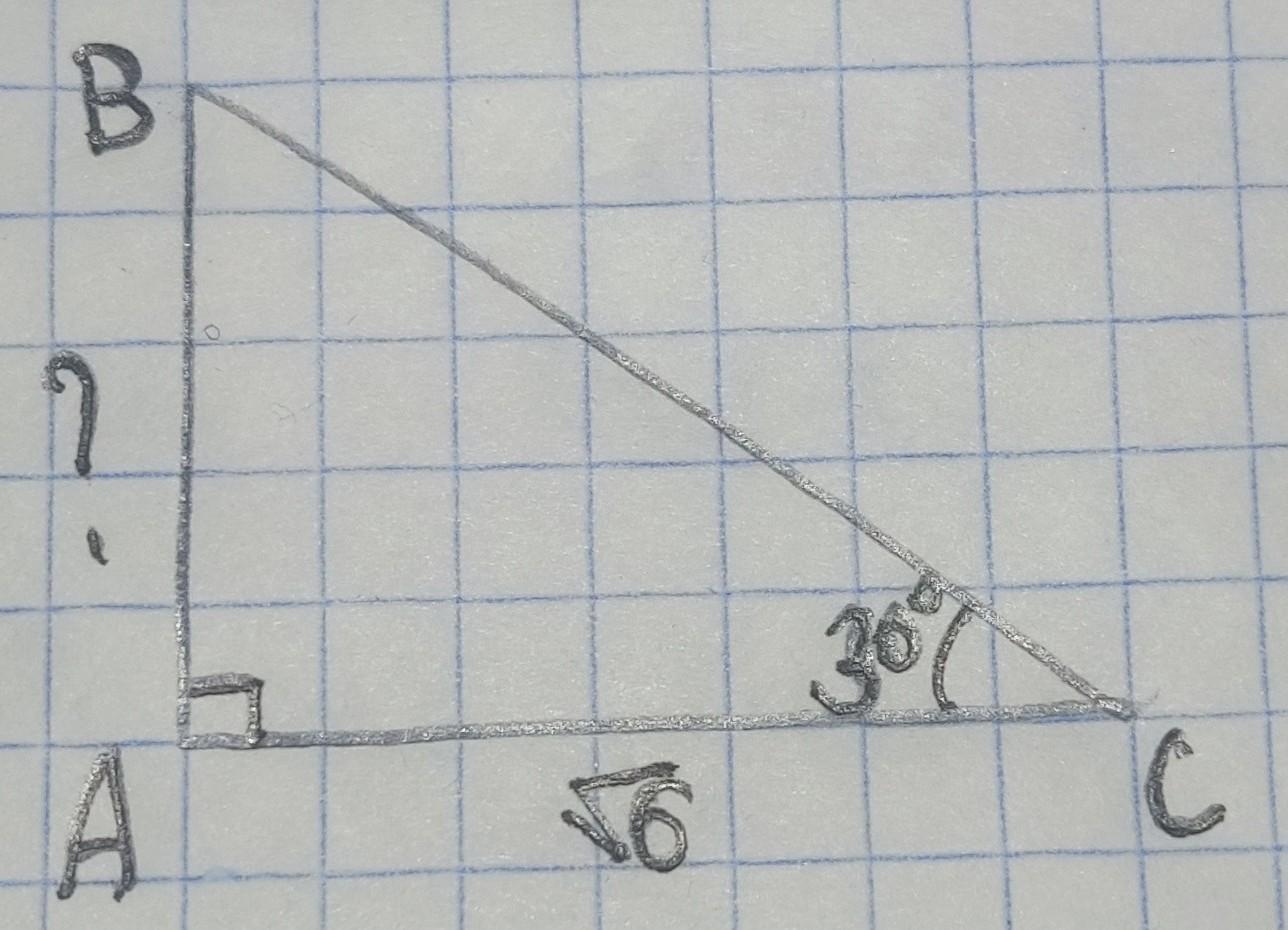
Дан прямоугольный треугольник. Угол С=30°, сторона АС=√6. Найти АВ​

Answer 1

Ответ: сторона АВ равна 2

Объяснение: сперва нужно использовать теорему синусов

a/sin(A) = b/sin(B) = c/sin(C)

a, b и c - стороны треугольника
A, B и C - соответствующие им углы

С равен 30°, так что мы можем записать:

a/sin(30°) = √6/sin(90°-30°)

sin(30°) = 1/2, а sin(90°-30°) = sin(60°) = √3/2, исходя из этого
a/(1/2) = √6/(√3/2)

Делим обе части на 1/2 и упрощаем

a = √6/√3

a = √(6/3)

a = √2

далее нужно использовать теорему Пифагора
Мы знаем, что сторона АС равна √6, а сторона АС равна √2
поэтому пишем
(AB)^2 = (AC)^2 - (BC)^2

(AB)^2 = (√6)^2 - (√2)^2

а далее просто упрощаем

(AB)^2 = 6 - 2

(AB)^2 = 4

AB = 2

Таким образом, сторона АВ равна 2