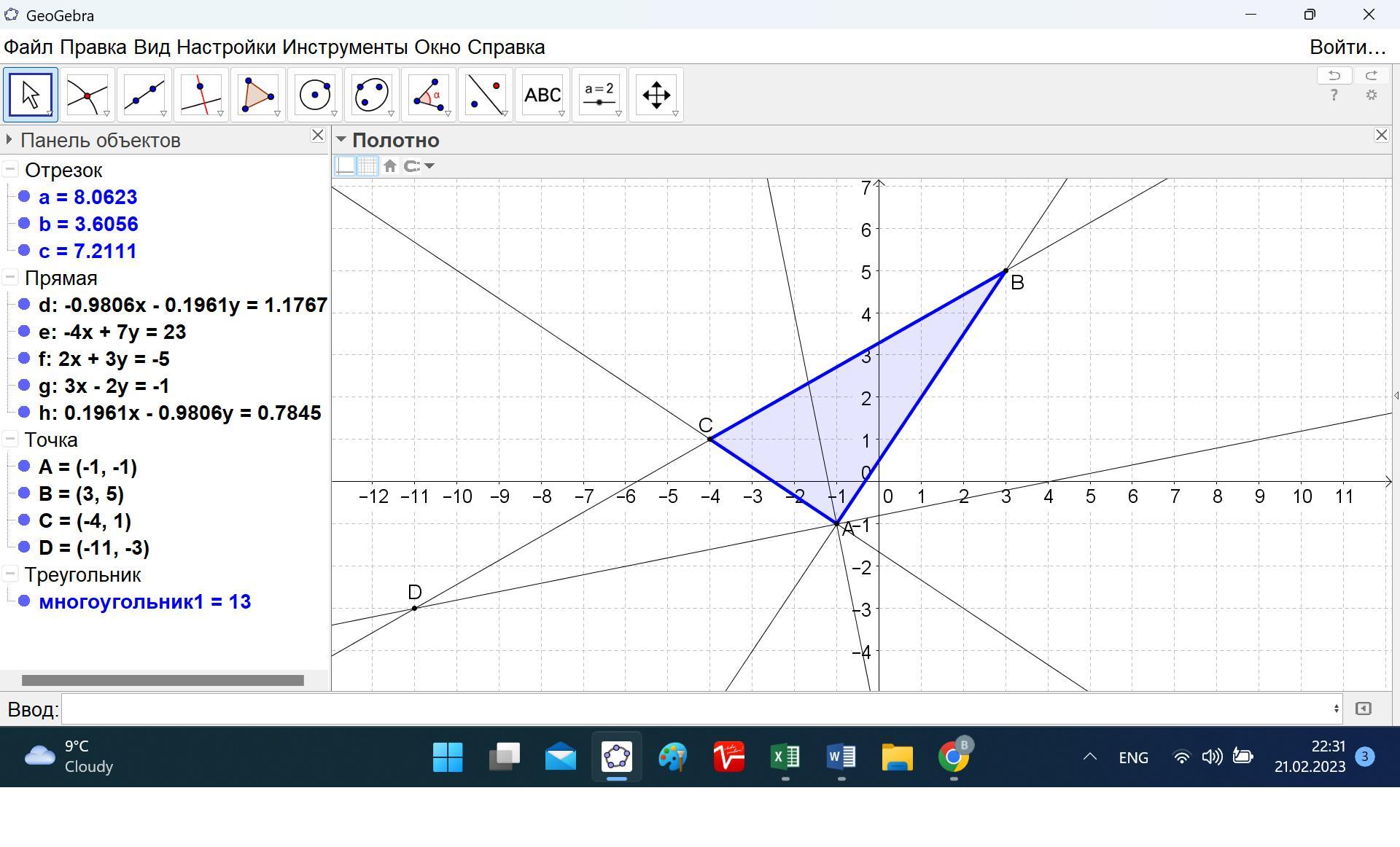
Дано вершини трикутника A(-1;-1), B(3;5), C(-4;1). Знайти точку перетину із продовженням сторони BC бісектриси його зовнішнього кута при вершині A.
Бажано не чат GPT
Ответы
Даны вершины треугольника A(-1; -1), B(3; 5), C(-4; 1).
Нахождение биссектрисы угла из свойств векторов.
Находим векторы из точки А.
AB = (3-(-1); (5-(-1)) = (4; 6).
AC = (-4-(-1); (1-(-1)) = (-3; 2).
Найдем биссектрису угла A.
Известно, что диагонали ромба делят углы пополам. Найдем орты векторов AC(-1,-3) и AB(-3,-1). Соответственно и на них, как на сторонах, построим ромб, диагональ которого AK, равную сумме ортов, можно взять в качестве направляющего вектора биссектрисы.
A(-1;-1), B(3;5), C(-4;1). AB=(4;6), AC=(-3;2).
|AB|=√(16+36)=√52=2√13. a=(4/(2√13)=((2/√13); (3/√13)).
|AC|=√(9+4)=√13. b=((-3/(√13); (2/(√13))).
Каноническое уравнение биссектрисы AK примет вид сучётом, что вектор AK=a+b=(-1/(√13); (5/(√13))
или (x + 1)/(-1/(√13)) = (y + 1)/(5/(√13)).
Уравнение биссектрисы АК: (x + 1)/(-1/(√13)) = (y + 1)/(5/(√13)).
Можно сократить на (√13).
(x + 1)/(-1) = (y + 1)/5.
5x + 5 = -y – 1,
Найдено уравнение внутреннего угла треугольника из вершины А: 5x + y + 6 = 0.
Биссектриса внешнего угла - это перпендикуляр к найденной биссектрисе.
Её уравнение x - 5y + C = 0 (коэффициенты А и В меняются на (В и (-А)). Подставим координаты точки A(-1; -1).
-1 - 5(-1) + C = 0, отсюда С = 1 - 5 = -4.
Уравнение x - 5y - 4 = 0.
Находим уравнение стороны ВС.
Вектор ВС = C(-4;1) - B(3;5) = (-7; -4).
Уравнение ВС: (x - 3)/(-7) = (y - 5)/(-4) или
4х - 12 = 7у - 35.
4х - 7у + 23 = 0.
Находим координаты искомой точки пересечения.
x - 5y - 4 = 0 х(-4) = -4х + 20у + 16 = 0
4х - 7у + 23 = 0 4х - 7у + 23 = 0
13у + 39 = 0. отсюда у = -39/13 = -3.
х = 4 + 5у = 4 + 5*(-3) = -11.
Ответ: точка D(-11; -3).