Предмет: Математика,
автор: denispehov
Допоможіть, будь ласка, терміново!!! Обчислити похідну
Приложения:
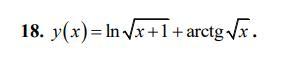
Ответы
Автор ответа:
0
Відповідь:
Покрокове пояснення:
розв'язання завдання додаю
Приложения:
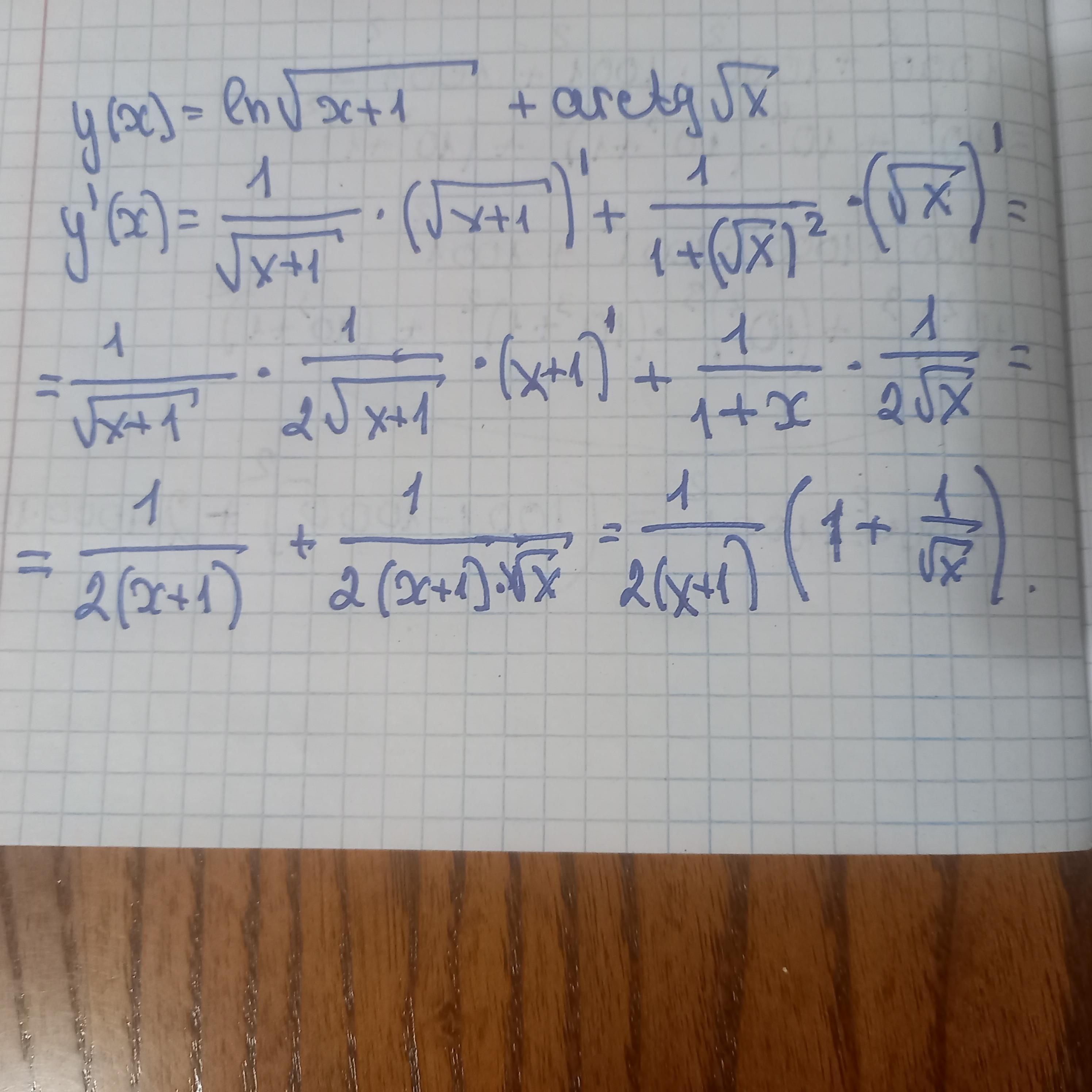
Автор ответа:
0
Ответ:
Найти производную .
Формулы :
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: vasilevicmarina20
Предмет: Английский язык,
автор: innazhyravel19031984
Предмет: Русский язык,
автор: c7804806
Предмет: История,
автор: makzanovailana65
Предмет: Математика,
автор: yuliamazur31232