Предмет: Геометрия,
автор: miraksenchuk
5) Дано: BM - медиана, AT-медиана. Доказать: BM+AT> 1/2(BC + AC)
Ответы
Автор ответа:
3
Ответ:
Доказано, что АТ + ВМ > 1/2 (АС + ВС)
Объяснение:
5) Дано: BM - медиана, AT-медиана. Доказать: BM+AT> 1/2(BC + AC)
Дано: ΔАВС;
ВМ и АТ - медианы;
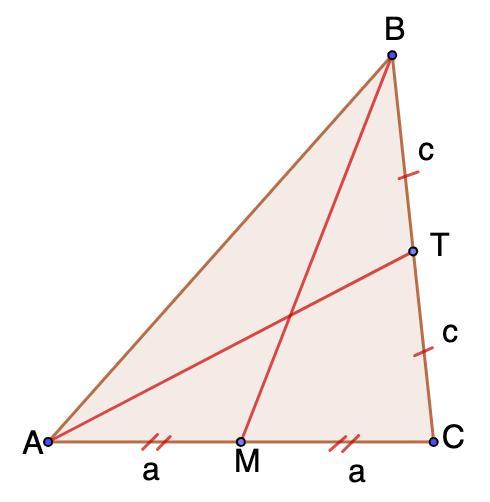
Доказать: BM + AT > 1/2 (BC + AC)
Доказательство:
Для удобства обозначим:
АМ = МС = (1/2) АС = а;
ВТ = ТС = (1/2) ВС = с.
Теорема о неравенстве треугольников:
- Каждая сторона треугольника больше разности двух других сторон.
Из ΔАТС:
АТ > AC - TC (1)
Из Δ МВС:
ВМ > ВС - МС (2)
- Неравенства одного знака можно складывать почленно.
Сложим неравенства (1) и (2):
АТ + ВМ > АС - ТС + ВС - МС
или
АТ + ВМ > 2a - c + 2c - a
АТ + ВМ > a + c
АТ + ВМ > (1/2) АС + (1/2) ВС
АТ + ВМ > 1/2 (АС + ВС)
#SPJ1
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: natapavlushnata
Предмет: История,
автор: plotnikr916
Предмет: Геометрия,
автор: dborisyuk06
Предмет: Русский язык,
автор: kiosamimiku00
Предмет: Математика,
автор: V0mp1r